Bi, Suzhi, et al. "Lyapunov-guided deep reinforcement learning for stable online computation offloading in mobile-edge computing networks." IEEE Transactions on Wireless Communications 20.11 (2021): 7519-7537.
机会计算卸载是提高动态边缘环境下移动边缘计算(MEC)网络计算性能的有效方法。
在本文中,我们考虑了一个多用户 MEC 网络,该网络具有随时间变化的无线信道和在连续时间帧中随机用户任务数据到达。
特别是,我们旨在设计一种在线计算负载算法,以在长期数据队列稳定性和平均功率约束下最大化网络数据处理能力。我们将问题表述为一个多阶段随机混合整数非线性规划 (MINLP) 问题,该问题共同决定了二进制卸载(每个用户在本地或在边缘服务器上计算任务)和系统资源分配决策在连续的时间范围内。
为了解决不同时间框架决策中的耦合问题,我们提出了一个名为 LyDROO 的新框架,它结合了 Lyapunov 优化和深度强化学习 (DRL) 的优势。
| 缩略单词 | 英文 | 中文 |
|---|---|---|
| MEC | mobile-edge computing | 移动边缘计算 |
| WD | wireless devices | 无线设备 |
| ES | edge server | 边缘服务器 |
| MINLP | mixed integer non-liner programming | 非线性整数规划 |
| DRL | deep reinforcement learning | 深度强化学习 |
预知识
一般来说,边缘计算系统有两种常见的加载模型:
- Binary:要求将计算任务的整个数据集作为一个整体在无线设备上本地处理或者在边缘服务器上远程处理
- Partial:允许在无线设备和边缘服务器上对数据集进行分区并行处理
Lyapunov
使用function来优化控制一个动态的系统,系统在某一个特定的时间节点的状态是可以使用一个多维向量来描述,而funcion则是对这个多维向量所表达的状态的一个非负的、标量的描述,我们常常采用:所有状态在各自权重下的平方和 来实行这一点。
如果系统的状态朝向一个不被期望的方向发展,那么function的数值就会变大,这样我们就可以将function沿着x轴的负方向逼近0使系统趋于稳定。
例
不妨将第t个time slot内产生的随机事件标为\(w(t) = [w_1(t),w_2(t),...,w_n(t)]\in \Omega^n\),每一个w是满足独立同分布的,\(\Omega\)为随机事件集合;系统在每个时间片使用的策略为\(\alpha(t) = [\alpha_1(t),...,\alpha_n(t)]\in A^m\),A为控制决策集合。
在第t个time slot,根绝发生的随机事件采取一系列的控制决策,所以对于优化的目标函数\(p(t)\)而言,会生成相应的数值 \[ p(t) = P(w(t),\alpha(t)) \] 系统中的一系列变量\(y_k(t)\)也会收到采取的决策的影响,可以描述为: \[ y_k(t)=Y_k(w(t),\alpha(t)) \] 在随机优化问题中,优化目标应该在time average中表现,所以优化问题标准式子为: \[ min_{\alpha(t)\in A^m}lim_{T\to \infty}\frac{1}{T}\sum_{t=0}^{T-1}E[p(t)] \]
\[ s.t.\space lim_{T\to \infty}\frac{1}{T}\sum_{t=0}^{T-1}E[y_k(t)]\leq0 \]
我们希望把满足这些长期的约束 条件所应当采取的操作分解到每每一个时间片内进行所以要建立虚拟队列
因此,对每一个约束条件\(y_k(t)\)定义一个对应的、初始值为0的队列\(Q_k(t)\) \[ Q_k(t+1)=max\{Q_k(t)+y_k(t),0\} \]
- 这里的Q并不是队列本身,而是队列的储备量
- 这里就可以看出队列有进有出,我们总是希望能处理的尽可能大于新抵达的,因为约束条件希望y不大于0
上式可以推到出 \[ lim_{T\to\infty}\frac{E(Q_k(T))}{T}=0 \] (5)将代替(3)中的约束成为新的约束
Lyapunov function 定义为: \[ L(\Theta(t))=\frac{1}{2}\sum_{k=1}^KQ_k(t)^2 \] 我们可以使用\(\Delta(\Theta(t))=L(\Theta(t+1))-L(\Theta(t))\)来表示从t到t+1全体队列的增加量,这也叫Lyapunov漂移
要在每一个时间片内求解\(\Delta(\Theta(t))+V·p(t)\)的最小值,也就是分别求两者的最小值,借助V来控制对二者的重视程度。
最后的最终式子为: \[ min_{\alpha(t)\in A^m}E[B+V·p(t)+\sum_{k=1}^KQ_k(t)y_k(t)|\Theta(t)] \]
Model & Problem Formulation
Model

如上图所示,我们考虑一个ES在相等的连续时间T中帮助N个WD
\(A^t_i\):我们定义\(A^t_i\)为在第t个时间点原始任务到达第\(i\)个WD的队列中,每个\(A_i\)是独立同分布的,并且\(E((A_i^t)^2) = \eta_i\),这里的\(\eta_i\)是已知的。
\(h_i^t\):我们定义在第i个WD和ES中间的信道增益为\(h_i^t\),该信道增益在一个时间帧内保持不变,但是在不同的帧之间独立变化
\(D_i^t\):表示在t时间帧内,第i个WD处理了\(D_i^t\)个bits,并在时间帧的最后输出
注意:这里只考虑Binary卸载规则,即智能选择WD或ES进行处理
\(x_i^t\):表示卸载决策
- 1:计算卸载,分配给ES
- 0:本地计算
本地处理的原始数据 (以位为单位) 和时间范围内消耗的能量是: \[ D^t_{i,L}=f_i^t\frac{T}{\phi} \]
\[ E_{i,L}t=\kappa(f^t_i)T \]
\[ \forall x_i^t=0 \]
- \(f_i^t\):本地CPU的处理数据速率
- \(\phi >0\):表示处理1bit 所需要的计算周期
- \(\kappa > 0\):表示计算能效参数
当我们把数据卸载到边缘处理的时候:
- \(P_i^t\):表示传输功率
- \(\tau^t_iT\):表示分配给第i个WD用于卸载的时间,\(\tau\in[0,1] \&\sum_{i=1}^N\tau_i^t \leq1\)
在时间范围内边缘处理的数据量为: \[ D_{i,O}^t=\frac{W\tau_i^tT}{v_u}log_2(1+\frac{E_{i,O}^th^t_i}{\tau^t_iTN_0}) \] \(v_u\geq 1\)表示计算开销,\(N_0\)表示噪声
所以我们表示在时间t内总共的比特计算和能量消耗: \[ D_i^t=(1-x)D_{i,L}+xD_{i,O} \]
\[ E_i^t=(1-x)E_{i,L}+xE_{i,O} \]

- \(r\)代表计算速度
- \(e\)代表功率消耗
- 我们假设T = 1
我们定义WD的队列长度为Q,那么对于一个队列:
\(t+1\)时刻的队列长度为t时刻的队列长度 - \(t\)时刻WD能处理的数据量 + 到来的数据量。(大于0的数) \[ Q_i(t+1) = max\{Q_i(t)-\tilde{D}^t_i+A^t_i,0\} \] 其中\(\tilde{D}^t_i=min(Q_i(t),D_i^t)\),即处理量最多就是队列中的数据量,因为我们假设这个队列是无限长的,所以\(D < Q\),所以动态队列被简化成以下形式: \[ Q_i(t+1) = Q_i(t)-D^t_i+A^t_i \] 根据利特尔定律,平均延迟与平均队列长度成正比。因此,强稳定的数据队列转化为每个任务数据bit的有限处理延迟。
问题表述
在本文中,我们旨在设计一种在线算法,以在数据队列稳定性和平均功率约束下,最大化所有 WD 的long-term average weighted sum compution rate。特别是,我们在每个时间帧内做出在线决策,我们在不假设知道随机信道条件和数据到达的未来情况下,优化任务卸载和特定时间帧的资源分配决策。
多层级随机MINLP问题表述如下图所示:
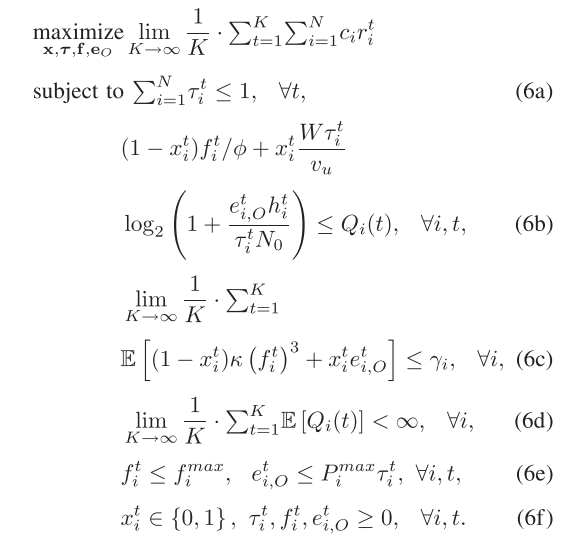
- \(c_i\)表示WD的固定权重,\(r^t_i\)代表WD在每一时刻的计算速度
- (6a)表示卸载时间限制,即在一个时间帧之内,每一个WD所获得的卸载时间比例的和不能超过1
- (6b) 对应于数据因果约束,数据处理不完:处理数据量\(D\) < 队列数据量\(Q\)
- (6c) 对应于平均功率约束,\(γ_i\) 是功率阈值。
- (6d) 是数据队列稳定性约束。
在不知道随机信道条件和未来数据到达量的情况下在时间帧之内做出决策是很难满足长期约束的。此外,快速变化的信道条件需要在每个短时间帧内(例如,在信道相干时间内)进行实时决策。
基于 LYAPUNOV 的多级 MINLP 解耦
我们应用 Lyapunov 优化将 (P1) 解耦为每帧确定性问题
为了解决平均功率约束(6c),文章定义了N个虚拟的能量队列\(Y_i(t)\),每个WD有一个虚拟队列,队列的初始化为0,更新公式为\(Y_i(t+1)=max(Y_i(t)+ve_i^t-v\gamma_i,0)\);\(v\)是正比例因子,\(e\)是在t时间帧的能量消耗。
这个队列可以被看做是具有随机“能量到达”和固定的“服务比率”,当虚拟能量队列稳定的时候,平均功率\(e\)不会超过\(\gamma\)
我们把数据队列\(Q\)和虚拟的能量队列\(Y\)放到一起,然后引入Lyapunov方程和Lyapunov漂移

为了在稳定队列\(Z(t)\)的同时最大化时间平均计算率,我们使用最小化drift-plus-penalty的办法。具体来说就是要在每个时间帧下最小化drift-plus-penalty的上界。drift-plus-penalty的表达式如下: \[ \Lambda(Z(t))=\Delta L(Z(t))-V·\sum_{i=1}^N\mathbb{E}\{c_ir_i^t|Z(t)\} \]
求drift-plus-penalty的上界
\[ Q_i(t+1)^2=Q_i(t)^2+2Q_i(t)(A_i^t-D_i^t)+(A_i^t-D_i^t)^2 \]
\[ Y_i(t+1)^2=Y_i(t)^2+2Y_i(t)(e_i^t-\gamma_i)+(e_i^t-\gamma_i)^2 \]
之后两边同时对N个队列进行求和,并将带有\(Q\)和\(Y\)的平方项合并到等式左侧,得到 \[ 0.5\sum_{i=1}^NQ_i(t+1)^2-0.5\sum_{i=1}^NQ_i(t)^2 =\sum_{i=1}^NQ_i(t)(A_i^t-D_i^t)+0.5\sum_{i=1}^N(A_i^t-D_i^t)^2 \] \[ 0.5\sum_{i=1}^NY_i(t+1)^2-0.5\sum_{i=1}^NY_i(t)^2=\sum_{i=1}^NY_i(t)(e_i^t-\gamma_i)+0.5\sum_{i=1}^N(e_i^t-\gamma_i)^2 \]
我们定义\(L(Q(t))=0.5\sum_{i=1}^NQ_i(t)^2\),并且\(\Delta L(Q(t)) = \mathbb{E}\{L(Q(t+1))-L(Q(t))|Z(t)\}\)
对15式子两边同时取期望可以得到 \[ \Delta L(Q(t)) \leq B_1 +\sum_{i=1}^NQ_i(t) \mathbb{E}\{A_i^t-D_i^t|Z(t)\} \] 类似的能获得: \[ \Delta L(Y(t)) \leq B_2 +\sum_{i=1}^NY_i(t) \mathbb{E}\{e_i^t-\gamma_i|Z(t)\} \] 结合(16)(17)能得到最后的式子 \[ \Delta L(Z(t)) \leq \hat{B}+\sum_{i=1}^NQ_i(t) \mathbb{E}\{A_i^t-D_i^t|Z(t)\} +\sum_{i=1}^NY_i(t) \mathbb{E}\{e_i^t-\gamma_i|Z(t)\} \] 因此这个drift-plus-penalty的上界就是等式右侧的式子。通过移除常数项,最后算法通过最大化如下式子来决定action: \[ \sum_{i=1}^N(Q_i(t) +Vc_i)r_i^t-\sum^N_{i=1}Y_i(t)e_i^t \]

最后将上文的式子,转化成了这个式子,可以看出,在这个式子中没有对于\(t\)的积分了,就简化了计算。
Lyapunov指导的DRL
在每一个时间帧中我们观察到的数据是 \[ \xi^t=\{h^t_i,Q_i(t),Y_i(t)\}_{i=1}^N \]
- \(h^t_i\):信道收益
- \(Q_i(t),Y_i(t)\):队列信息
通过这个我们得出最后的控制动作:是否卸载、持续资源分配 \[ \{x^t,y^t\} \]
\[ y^t=\{\tau_i^t,f_i^t,e_{i,O}^t,r_{i,O}^t\} \]
我们发现,虽然最后的公式不是一个凸优化,但是如果\(X\)的状态是确定的,那么上述公式就会转变成凸优化,所以我们要先去确定\(X\)。一般来说,枚举获得\(X\)是需要枚举\(N^2\)个决策,这样的复杂度很高,所以我们使用DRL来构建一个策略\(\pi\),通过这个策略来将输入映射到最优的动作\(x^t\)上。

actor:
接受输入的\(\xi\)并输出候选的卸载动作\(x_i^t\)
Actor模块由一个DNN和一个动作量化器组成。 在第 t 个时间帧的开始,我们将 DNN 的参数表示为\(θ_t\),当\(t =1\)时按照标准正态分布随机初始化。以观测值\(ξ_t\)作为输入,DNN 输出一个松弛的卸载决策\(\hat{x}^t\in [0, 1]^N\),这个决策稍后将被量化为可行的二元动作。此时是连续变量
之后将连续的\(\hat{x}^t\)量化为可行的卸载动作\(\Omega_t\),\(x_j^t\in\{0,1\}^N\),为离散变量数组
对于前\(\frac{M_t}{2}\)个变量,我们按照如下策略(NOP)进行赋值:
对于第一个变量,很简单的赋值就是,如果其大于0.5,就是1,否则就是0;剩下的变量将其按照到0.5的距离进行有大到小的排序,获得\(\hat{x}_{(n)}^t\)序列,这些将会用做判断阈值:

对于剩下的一半变量,我们给其一个噪声,然后用sigmoid进行激活:\(x^t=sigmoid(x^t+n)\),激活后重复前一半的步骤
第一次得到的是一个连续值一维数组,每一个用户对应一个连续值;之后变成了一个二维数组,每一个用户对应着一维数组(每个数组的元素都是离散值)
critic:
测评输出的\(x_i^t\)并选择最优的卸载动作\(x^t\)。
其实就是通过最后的方程进行反向推导,此时已经知道\(x\)的值了,就可以进行凸函数优化了。 \[ x^t=arg max_{x_j^t\in \Omega_t}G(x_j^t,\xi^t) \]
policy update:
提升actor模块的策略
queue:
在卸载策略已经执行过后更新系统队列