- BC-based Trusted Trafic Offloading in SAGIN
- 预备知识(PBFT、MDP、AC算法)
- 论文解读
- A Fast BC-based FL Framework with Compressed Communications
- 预备知识(FL过程)
- 论文解读
Blockchain-based Trusted Traffic Offloading in SAGIN:FRL Approach
网址:https://ieeexplore.ieee.org/document/9918062
F. Tang, C. Wen, L. Luo, M. Zhao and N. Kato, "Blockchain-based Trusted Traffic Offloading in Space-Air-Ground Integrated Networks (SAGIN): A Federated Reinforcement Learning Approach," in IEEE Journal on Selected Areas in Communications, 2022, doi: 10.1109/JSAC.2022.3213317.
Preliminaries
PBFT
在讨论PBFT之前,我需要先讲述一下区块链网络中的共识机制。
由于区块链是一个完全公开的数据链,所有人都可以匿名接入,所以共识机制的出现就是为了防止区块链的不稳定和被攻击。按大白话来说:共识机制就是如何网络中的所有节点达成共识,获得一样的结果。普遍的共识机制有PoW,PoS等等。
在区块链中:一个矿工挖矿之后,必须通过共识才可以上链,上链即意味着:可以存储到所有的账本之中,这项交易被记录。
这里讲一下PBFT算法(实用拜占庭容错算法)
这个算法的本质就是:任何一个节点收到了Leader节点的消息,都要去怀疑这个命令是否正确,而为了能确保消息的准确,我要和团队中的其他节点进行确认,只有大多数人认为Leader的命令是正确的时候,节点才会去执行这个命令。
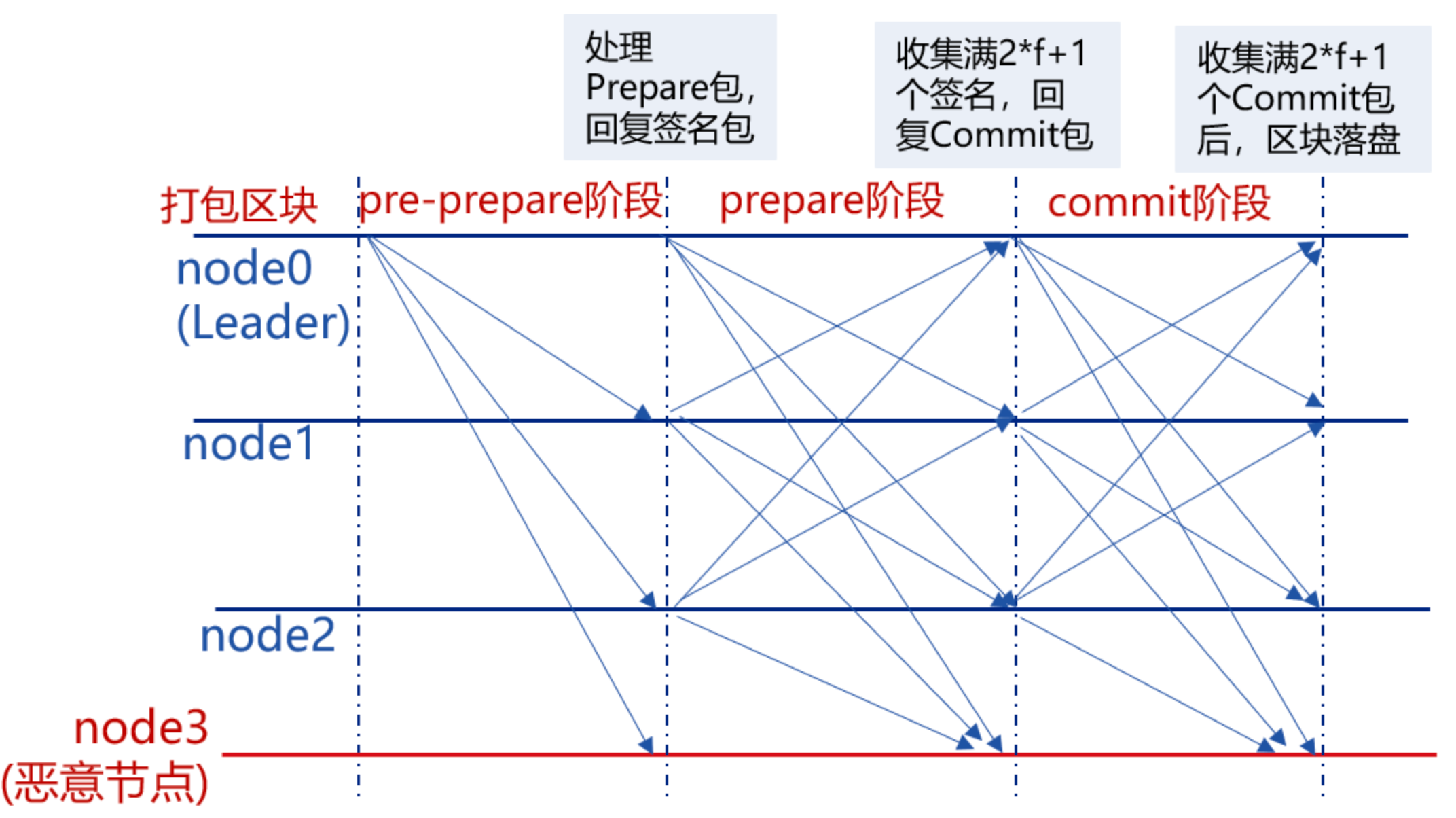
Pre-prepare:负责执行区块,产生签名包,并将签名包广播给所有共识节点;
\(<<PRE-PREPARE,v,n,d>,m>\)
其中v是视图数,这个阶段为了给request排序
Prepare:负责收集签名包,某节点收集满
2*f+1的签名包后,表明自身达到可以提交区块的状态,开始广播Commit包;\(<PREPARE,v,n,d,i>\)
从节点告诉其他节点:表明自己已经收到了Leader的建议,然后将该建议分发给所有节点,去核实信息。
每一个节点达到prepare状态时,并不知道其他节点的状态(恶意节点会给不同的节点发送不同的信息),所以还需要广播commit包
Commit:负责收集Commit包,某节点收集满
2*f+1的Commit包后,直接将本地缓存的最新区块提交到数据库。
收集到prepare包,表明自己已经收到了和大多数节点一致的主节点命令,我可以在本地提交;广播给大家之后,收集到2f+1个commit包之后,就表明大多数已经在本地提交,此时可以区块落盘。
在这里需要对request的序号达成共识,这些节点可能会在不同的视图中提交。
视图:
如果说主节点宕机或者主节点是恶意节点,就需要进行视图切换。
从节点发现主节点有问题,就需要广播切换视图的数据包,只要从节点发现就需要发送该数据包。新的主节点(主节点候选人)收到2f+1个切换视图的数据包,就会进行视图切换。该新主节点就会广播NewView数据包,从节点收到数据包之后进行校验,校验成功之后会进入新的视图。
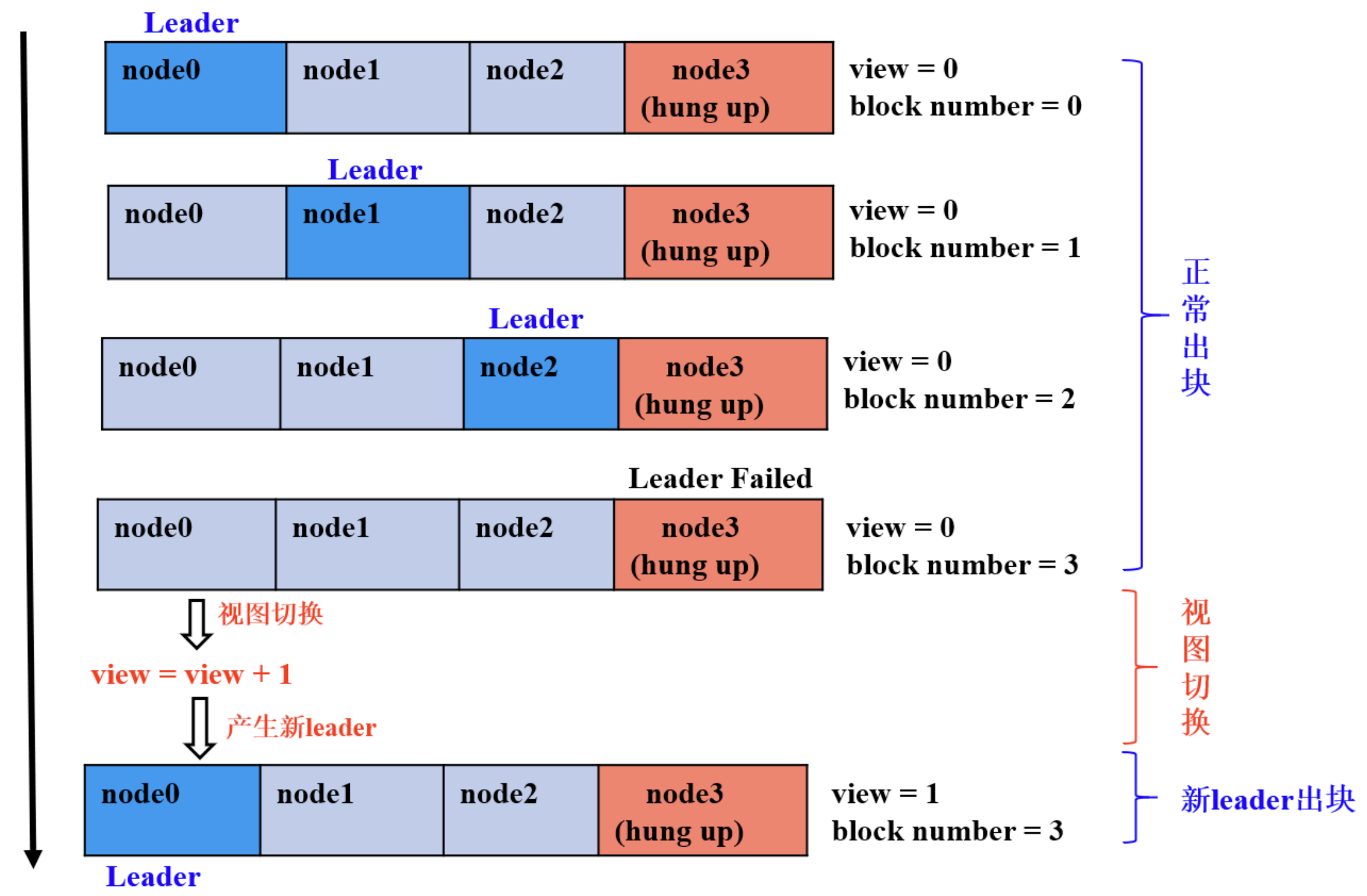
在上图中node3是恶意节点,在0号view中,node0-2分别当Leader节点,此时是没有问题的,但是当node3成为Leader节点之后,其他节点发现主节点是恶意节点,此时触发视图切换,重新选择主节点,就变成了1号view,此时node0成为了主节点。
马尔科夫决策过程 MDP
第一个概念是马尔科夫性:
指该系统的下一个状态\(s_{t+1}\)只与当前状态\(s_t\)有关,和之前的状态没有关系。公式表示:\(P[s_{t+1}|s_t] = P[s_{t+1}|s_1,...,s_t]\)
第二个概念是马尔科夫过程:
该过程的定义:马尔科夫过程是一个二元组\((S,P)\),且满足:\(S\)是有限状态集合, \(P\)是状态转移概率。状态转移概率矩阵为:\(P = \begin{bmatrix} P_{11} & ...&P_{1n} \\ . & . & .\\P_{n1} & ...&P_{nn} \end{bmatrix}\)
具体来说就是每一个状态转换到下一个不同的状态都会自己不同的概率,只知道开始与结束是不能确定中间的过程的。比如说一个学生从课1 到 睡觉,之间就会有很多不同的状态序列。

第三个概念是马尔科夫决策过程
马尔科夫决策过程由元组\((S,A,P,R,γ)\)描述,其中:\(S\)为有限的状态集, $A $为有限的动作集, \(P\) 为状态转移概率,$ R$为回报函数, \(γ\) 为折扣因子,用来计算累积回报。
注意:跟马尔科夫过程的不同点是,马尔科夫决策过程的状态转移概率是包含动作的。

在上图中,学生总共有五个状态\(S = \{s_1,s_2,s_3,s_4,s_5\}\),动作也有五个\(A=\{玩、退出、学习、发论文、睡觉\}\),其中每一个动作都会有一个立即回报R$
一般来说,在马尔科夫决策过程上的强化学习目标都是寻找最优策略。策略\(\pi\)就是状态到动作的映射,它是指给定状态\(s\)时,动作集的一个分布,即\(\pi(a|s)=p[A_t=a|S_t=s]\)
含义是:策略\(π\)在每个状态\(s\)指定一个动作的概率。如果给出的策略\(π\)是确定性的,那么策略\(π\)在每个状态\(s\)指定一个确定的动作。
例如:其中一个学生的策略为玩\(π_1(玩|s_1)=0.8\),是指该学生在状态\(s1\)时玩的概率为0.8,不玩的概率是0.2,显然这个学生更喜欢玩。
强化学习的目标就是找到最优的策略,这里的策略是指得到的总回报最大
累计回报计算公式:\(G_t=R_{t+1}+\gamma R_{t+2}+...=\sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\)
讲解一下\(\gamma\)的用处:
为游戏里,越接近游戏开始处的奖励,就越容易获得;而随着游戏的进行,后面的奖励就没有那么容易拿到了。
把智能体想成一只小老鼠,对手是只猫。它的目标就是在被猫吃掉之前,吃到最多的奶酪。

就像图中,离老鼠最近的奶酪很容易吃,而从猫眼皮底下顺走奶酪就难了。离猫越近,就越危险。
结果就是,从猫身旁获取的奖励会打折扣:吃到的可能性小,就算奶酪放得很密集也没用。
假设从状态\(s_1\)出发,给定了策略\(\pi\),那么学生的状态序列可能为:
\(s_1\to s_2 \to s_3 \to s_4\to s_5\);\(s_1 \to s_2 \to s_3 \to s_5\)
所以说在给定了策略\(\pi\)后,由于过程的不确定,那么\(G_1\)也有不同的值,为了更好的评价状态\(s_1\)的价值,我们需要定义一个确定的量来表示该价值,所以我们利用期望来作为状态值函数的定义。
状态值函数(在某个状态有多好):
当智能体采用策略\(π\)时,累积回报服从一个分布,累积回报在状态\(s\)处的期望值定义为状态-值函数: \[ v_\pi(s)= E_\pi[\sum^{\infty}_{k=0}\gamma_kR_{t+k+1}|S_t=s] \] 这个含义就是在状态\(s\)上,到最后目标状态的所有路径的回报期望值。
注意:状态值函数是与策略\(π\)相对应的,这是因为策略\(π\)决定了累积回报\(G\)的状态分布。
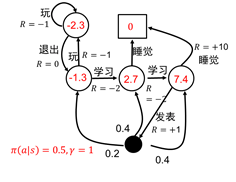
红色部分是每一个状态的状态值函数。
状态-行为值函数(在某个状态选择某个动作有多好): \[ q_\pi(s,a)= E_\pi[\sum^{\infty}_{k=0}\gamma_kR_{t+k+1}|S_t=s, A_t=a] \]
Actor-Critic算法
我们将 Actor-Critic 分为两个部分:Actor(策略网络)和 Critic(价值网络)
- Actor 要做的是与环境交互,并在 Critic 价值函数的指导下用策略梯度学习一个更好的策略。
- Critic 要做的是通过 Actor 与环境交互收集的数据学习一个价值函数,这个价值函数会用于判断在当前状态什么动作是好的,什么动作不是好的,进而帮助 Actor 进行策略更新。
Actor 的更新采用策略梯度的原则,那 Critic 如何更新呢?
我们将 Critic 价值网络表示为\(V_\omega\),参数为\(\omega\)。于是,我们可以采取时序差分残差的学习方式,对于单个数据定义如下价值函数的损失函数: \[ L(\omega)=\frac{1}{2}(r+\gamma V_\omega(s_{t+1})-V_\omega (s_t))^2 \] 与 DQN 中一样,我们采取类似于目标网络的方法,将上式中\(r+\gamma V_\omega(s_{t+1})\)作为时序差分目标,不会产生梯度来更新价值函数。因此,价值函数的梯度为: \[ \nabla_\omega L(\omega)=-(r+\gamma V_\omega(s_{t+1})-V_\omega (s_t))\nabla_\omega V_\omega(s_t) \] 然后使用梯度下降方法来更新 Critic 价值网络参数即可。
Actor-Critic 算法的具体流程如下:
- 初始化策略网络参数\(\theta\),价值网络参数\(\omega\)
- for 序列\(e=1\to E\) do :
- 用当前策略\(\pi_{\theta}\)采样轨迹\(\{s_1,a_1,r_1...\}\)
- 为每一步数据计算: \(\delta_t=r_t +\gamma V_\omega(s_{t+1})-V_\omega (s_t)\)
- 更新价值参数\(\omega=\omega + \alpha_\omega \sum_t\delta_t \nabla_\omega V_\omega(s_t)\)
- 更新策略参数\(\theta = \theta + \alpha_{\theta}\sum_t\delta_t \nabla_\omega log\pi_{\theta}(a_t|s_t)\)
- end for
论文解读
遇到的问题
- 如今单靠地面无线技术来满足超高服务质量需求是一个挑战,以为预计到2023年,将有超过5000亿个物联网设备投入使用,这就导致了不同物联网设备之间的数据和信息交换数量激增,但是由于地面上的网段的覆盖范围和容量有限,没有办法对偏远或非地面的设备提供稳定的网络接入。
- 为了解决上述问题,研究人员选择了使用
Space-Air-Ground网络来缓解上述压力。但是由于卫星和无人机的高机动性和异构性,又会导致没办法用基于固定规则的流量卸载方法来处理该问题。这里使用到了强化学习方法来取代正常的流量卸载方法。 - 由于SAGIN巨大的网络空间,传统的机器学习需要全局数据将成为较大的开销,同时原始训练数据的交换将显著增加隐私担忧。
- 研究人员选择使用联邦学习来缓解上述问题,但是中心服务器的入侵也会导致联邦学习的学习效果下降。
- 该模型引入了区块链来保证联邦学习不会受到恶意入侵的剧烈影响。
场景描述
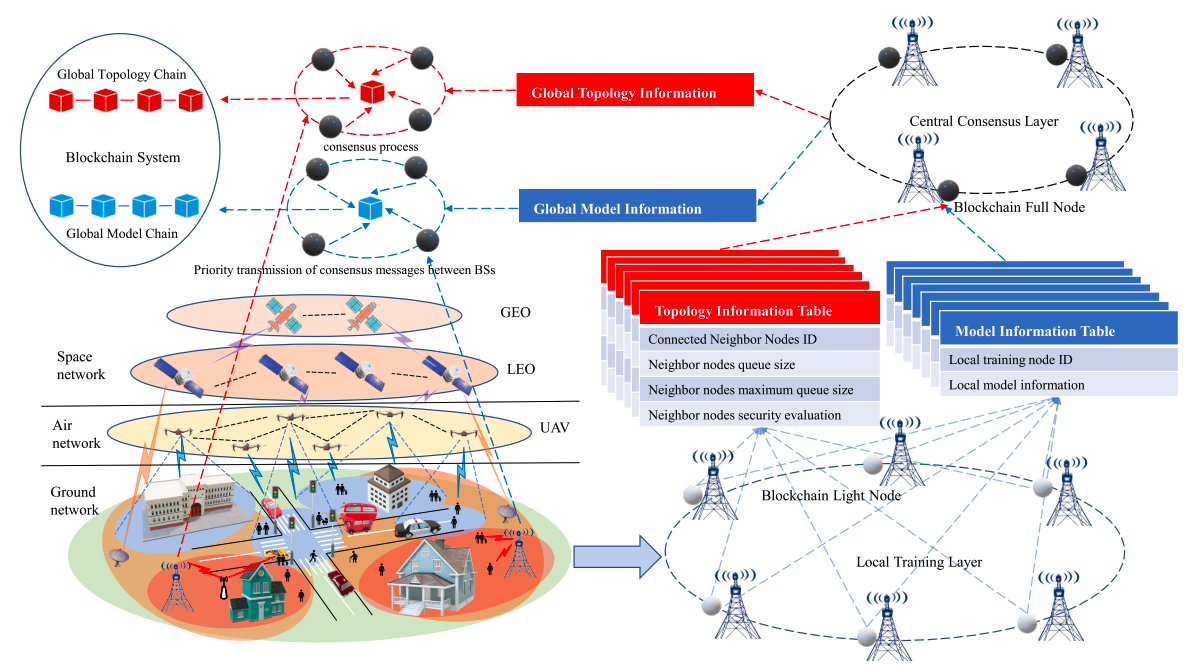
地面上有两种设备:一个是用户的设备:UE,一个是类似基站的东西:BS
空中有一种设备:无人机UAV
太空上有两个设备:低轨卫星LEO,同步卫星GEO
我们现在要做的就是:两个UE设备要进行数据交换,通过强化学习的方法来找到一个最优的路径来连接两个UE,无论是卸载到BS还是UAV还是LEO、GEO,总之目的就是数据交换。
部分安全分数较高的BS作为本地训练节点,BS中安全分数最高的一部分是中心共识节点。
UAV、LEO、GEO都是区块链的轻节点(不存全部的信息)
创新点
为了实现网络信息在节点间的安全共享,引入了区块链技术。
引入联邦学习技术来保护数据隐私,减少SAGIN中传输原始数据的开销。
提出了一种新的基于区块链的联邦学习架构。
基于上述框架,提出了一种双区块链结构。
为了解决流量卸载中的安全节点选择问题,设计了一种节点安全评估机制。
提出了一种共识节点选择机制,然后在此基础上提出了一种改进的实用拜占庭容错算法(EPBFT)。
我们将SAGIN中基于区块链的流量卸载问题抽象为MDP,并提出了基于RL的方法来解决该问题。
我们提出了一种无模型的A3C算法来动态学习网络拓扑结构,并做出优化决策,以使系统总时延最小
总体框架
本地训练层
本地训练层由地上的BS组成,当BS超过负载的时候,系统启用卸载方案,本地节点会收集相邻节点的拓扑信息(包含连通性、安全评估信息)
中心共识层
通过安全评估机制选择的BS节点组成中心共识层,该层收集本地训练层上传的拓扑信息和局部模型参数,并对训练结果进行评估。中心共识层都是共识节点,来作为分布式的区块链来运行,该层的节点可以通过区块链与其他节点共享模型参数。
区块链系统
该文章提出了一个双区块链系统,一个用来存储网络的拓扑信息,一个用来存储模型信息。中心共识节点都作为区块链的全节点,参与共识过程,本地训练节点和其他设备节点(UAV等)都是轻节点,并不参与共识
- 拓扑链:拓扑信息包括:本地训练节点一跳、两跳的设备集(BS、UAV、GEO、LEO);节点队列;安全评估信息。共识层会将其打包到区块链中,在模型验证中起到必不可少的作用
- 模型链:本地训练节点将本地模型上传,共识层进行聚合然后打包成块,添加到区块链中。此外共识层还需要对本地模型进行验证来作为安全评估。
系统模型
文章将整个SAGIN看成了一个加权有向图,节点包括各个设备,加权的赋值为0,1(0为两个设备没有建立连接,1代表两个设备建立了连接)。系统节点分为UN和RN,UN就是UE(生成数据包并将其传输到其他的UE),RN就是无人机等中继节点(relay nodes)。在每一个时间\(t\),每一个UE会生成一个大小为\((\mu, \omega^2)\)正态分布的数据包,按照一个预设好的路径传输给另一个UE:\(path=\{un_s \to un_d\}\)
通信模型
UAV-Ground通信传输速率:即BS和UAV的通信,公式如下 \[ tr_t^{UB}=W_{UB}log_2(1+ \frac{P_{UB}·10^{-\frac{L}{10}}}{\sigma^2_{UB}}) \] \(W_{ub}\)表示无人机与BS之间的信道带宽,\(P_{ub}\)表示无人机与BS之间的发射功率,\(σ^2_{UB}\)表示无人机与BS之间的噪声功率,\(L\)表示无人机与BS之间的平均路径损耗。
UAV-Satellite通信传输速率:这里需要考虑雨水对信号的影响。由于无人机的运动相比于卫星的运动很小,所以可以看做UAV的运动是静止的。 \[ tr_t^{US}=W_{US}log_2(1+ \frac{P_{US}·I^2_{US}}{\sigma^2_{US}}) \] \(I_{US}\)表示雨水对信号的缩减(基于Weibull)。
区块链延迟模型
区块链中的延迟主要是共识延迟和节点更新延迟,文章定义每m次共识之后需要进行一次节点更新,所以区块链的平均延迟为 \[ T_c^b(t)=\frac{MT_{con}(t)+T_{upd}(t)}{M} \] 为了保证避免恶意节点对于SAGIN的影响,我们需要对平均延迟做一个约束,即\(T_c^b(t)\leq(T_c^b)_{min}\),\((T_c^b)_{min}\)是为了安全所设定的限制。
流量卸载延迟模型
端到端时延是源节点到目的节点路径上所有时延分量的总和,分为链路上时延和排队时延两个分量。 另外,链路上的时延又分为传播时延和传输时延。
传播时延:信号在传播过程中的延迟
传输时延:由于信号信息是有大小的,传输这个数据所需要的延迟
\[ T_{path_{i,j}}=\frac{x_{i,j}}{\iota}+\frac{l}{tr_t^{i,j}}+\eta \frac{l}{tr_t^{i,j}} \]
其中\(x_{i,j}\)是节点之间的物理距离,\(\iota\)是信号的物理传输速度;\(l\)是信号的长度,\(tr_t^{i,j}\)是节点\(i\)和节点\(j\)之间的传输速率,\(\eta\)是排队的位次
- 第一项:两节点之间的传播时延
- 第二项:本信号的传输时延
- 第三项:排队时延
最终的问题描述就是,我们需要找到一个路径使得在约束条件下,流量卸载的延迟是最小的。
节点安全评估和共识机制
节点安全评估
我们假设恶意节点有以下三种行为
- 恶意节点有一定的几率丢包
- 恶意节点可能不按照指定的路由路径或卸载方案传输包
- 恶意节点可能将性能不佳的模型上传中心共识层
针对上述三种行为,文章给出了以下三个安全评估指标
计算节点的投递率,投递率越高该节点丢包几率越小,越安全:\(\frac{传出数量}{传入数量}\)
本地训练节点接收到数据包时,检测最后一跳是否采取了最优路径,如果没有采用,就检测错误,将该值归一化
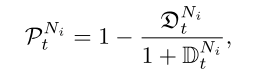
通过测试上传模型的性能来评估是否为恶意节点,将不正确的模型与正确模型相比,然后归一化。
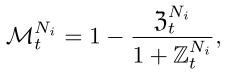
最后将三个值相乘,得出最后的安全评估指数,由于三个值的区间全是\((0,1]\),所以最后的值也是\((0,1]\)
共识机制EPBFT
传统的PBFT的主节点选择是利用残差法,但残差法对主节点的选择具有随意性和不可控性,不能保证所选主节点的安全性。
这个算法与PBFT的区别就是增加了动态添加和删除节点的功能。
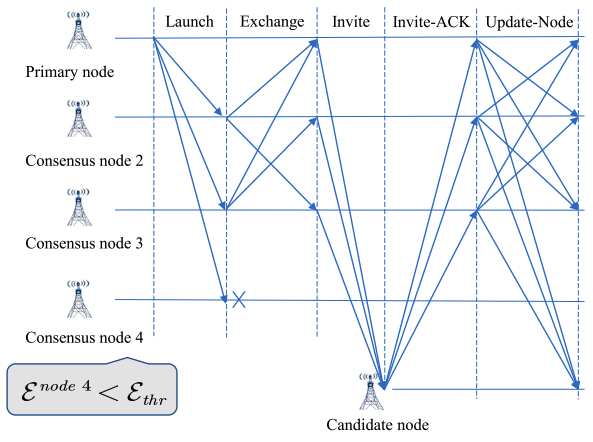
更新共识节点步骤:
- 在共识M次之后,启动节点更新进程,主节点(node 1)将安全评估值最低的共识节点发送给其他节点(node 4)
- 在共识节点收到该消息之后,向其他共识节点发送消息,如果收到
2f+1以上的消息(包括第一步主节点发送的消息),将公式列表更新 - 如果删除成功,那么所有节点向安全值最高的节点发送INVITE消息
- 候选人收到消息之后,向每一个向他发送INVITE的节点发送INVITE-ACK回复
- 共识节点收到ACK消息之后,共识节点向其他节点发送UPDATE消息,每一个共识节点收到
2f+1个UPDATE消息,将候选节点正式变成共识节点
主节点的选择:
选择安全值最高的节点作为主节点,当要切换视图的时候,我们从中心节点重新选择安全值最高的节点作为主节点
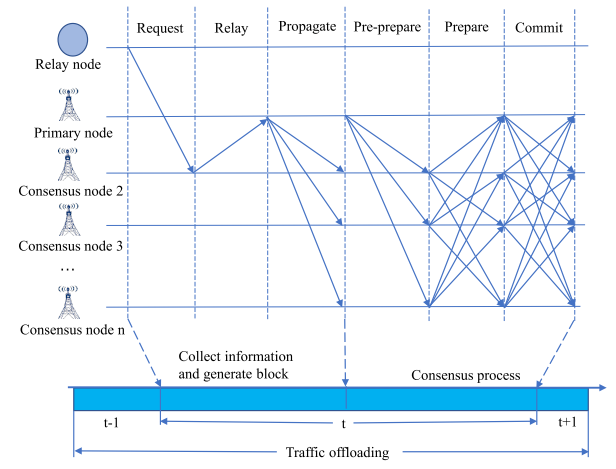
共识步骤:
中继节点(BS、UAV、SAT)向最近的共识节点发送自己的信息
共识节点收到之后向主节点打包发送
主节点将该信息广播给其他共识,主节点验证MAC之后,开始PBFT传统过程
同时为了加快共识进程,我们把共识信息设置BS传输的最高优先级。
联邦强化学习下的流量卸载
MDP
状态空间
一个多维数组,包含节点周围所有的一跳和两跳邻居的相关信息
动作空间
\(a(t) = \{0,RN_i\}\),0代表着采用最开始的路由路径,\(RN\)代表着根据写在决策来卸载到邻居节点如BS、UAV、SAT
转移概率
由于无人机等带来的不确定性,这一方面是很难建模的,所以要利用机器学习
回报函数
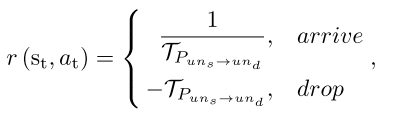
如果消息传到了目的节点,那么取其倒数,传播事件越长回报越小
如果消息没有达到目的节点,那么直接取反,回报函数会随着时间显著减小
价值函数
和MDP一样,取其期望。
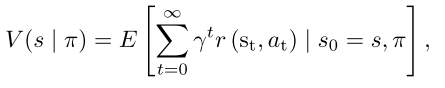
决策
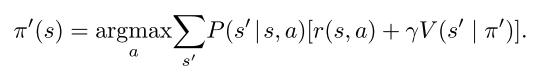
在状态\(s\)选择\(s'\)的概率×(在s状态选择a动作的回报 + 在\(s'\) 的状态下采用\(\pi'\)的价值)
在状态S下选择动作A的最优策略π,使包延迟最小
BFA3C 联邦强化学习
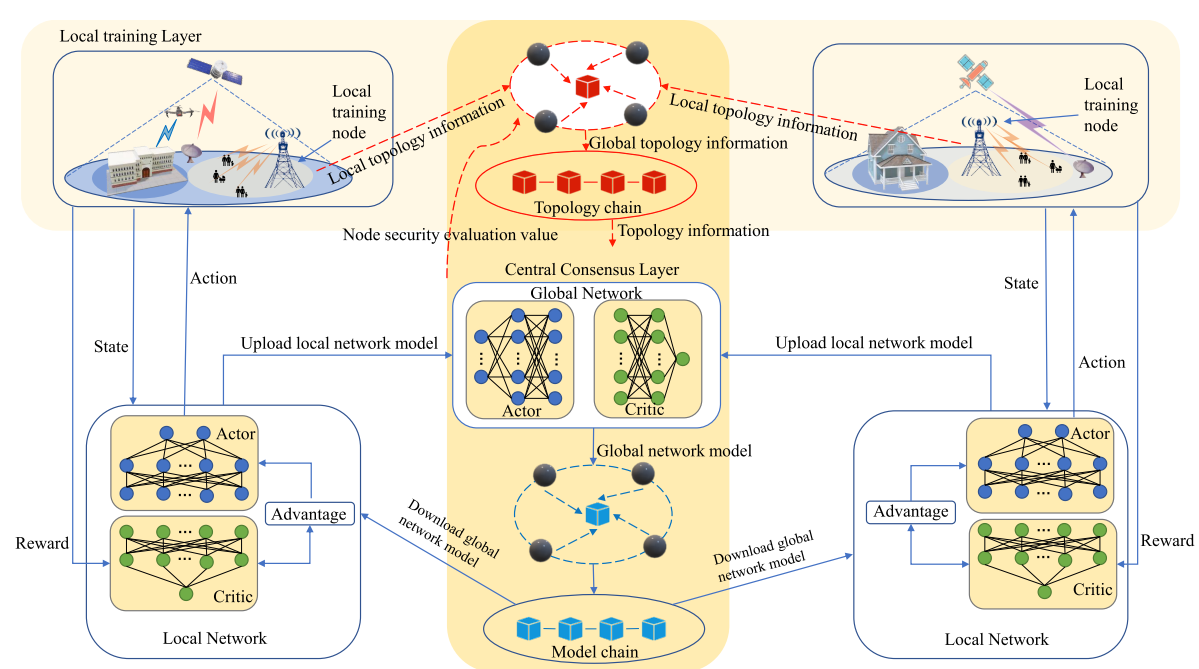
框架
BFA3C有一个全局神经网络模型(即中心权重矩阵),它包含一个Actor网络和一个Critic网络,以及几个由局部Actor网络和局部Critic网络组成的局部网络模型(即局部权重矩阵)。
每个局部训练节点都有其局部网络,局部网络单独探索环境
∆ 并周期性地将局部网络学习的结果馈送到中心共识层。 同时将本地网获取的拓扑信息上传到中心共识层。 该拓扑信息在共识处理后添加到拓扑链中。
∆ 中心共识层聚合上传的本地模型,并将全局模型打包到一个块中,将其添加到模型链中。
∆ 局部训练节点从模型链中获取最新的全局模型,并对局部模型进行更新。
此外,中心共识层从拓扑链中获取拓扑信息作为模型输入,对本地模型进行验证,验证结果将添加到拓扑链中,更新节点安全评估信息。
BFA3C流量卸载算法如下:
该算法首先在中心共识层初始化Actor网络和Critic网络参数。
当本地训练节点开始接收对传输包的请求时,本地训练节点从模型链中获取相应的预训练模型并进行在线学习。
本地训练节点通过收集来自周围邻近节点的信息作为模型的输入,根据本地参与者网络中的策略选择用于卸载决策的动作。
局部评价网络生成最后一个时间序列位置\(s_t\)的奖励值,并计算每个时刻的累积折扣函数。 最后,分别计算了局部Actor和Critic网络的梯度。
在本地训练时,作为运行BFA3C的本地训练节点进行异步训练,并周期性地将新的模型参数上传到中心控制层。
中心共识节点在从本地训练节点接收到本地网络模型后,中心共识层从拓扑信息链中获取拓扑信息,以验证本地模型的性能。
中心共识层根据模型的性能更新本地训练节点的安全评估值。 中心共识层在整合局部模型后,将全局模型放入区块,执行共识过程。
最后,局部学习节点从模型链中获取最新的全局网络模型,并更新其局部网络模型。
总结


Handscript(informal) :
场景大概就是两个UE要进行通信,但是由于地面上的基站覆盖面比较小,所以引入了UAV和Sat设备进行流量卸载。
每一个UE产生信息之后会传输给中继节点(BS,UAV,SAT),中继节点也可以传输给下一个中继节点,最后传给终点UE。
每个信息的传输路径是有一个最初设计的路径,还有一个卸载路径:由训练节点训练的模型通过联邦学习生成的,模型的目的是使得延迟最小。
每一个BS训练节点在每一个时隙t(一段时间)进行模型更新,因为这是一个动态异构的拓扑结构,所以要一直更新,同时每一个时隙t中都要计算每一个节点的安全评估。
联邦学习并不是训练一次就结束了:他是下载模型,然后训练更新之后,上传聚合之后,再下载,再训练……
所以说,每一个时隙t中都要进行拓扑结构的更新,模型的训练。期间数据的传输按照模型链上的最新模型进行指导。
拓扑结构的更新是每一个BS(训练节点)收集其连接的一跳、二跳的BS、UAV、SAT。(并不是全连接)
??貌似只有训练节点才有安全值??
在每一次本地训练节点收到传输的请求的时候,它首先从模型链中获取模型,然后将周围邻居节点的信息作为输入,获得决策动作。
A Fast BC-based FL Framework with Compressed Communications
网址:https://ieeexplore.ieee.org/document/9917527
L. Cui, X. Su and Y. Zhou, "A Fast Blockchain-based Federated Learning Framework with Compressed Communications," in IEEE Journal on Selected Areas in Communications, 2022, doi: 10.1109/JSAC.2022.3213345.
Preliminaries
FL过程
在联邦学习中,数据样本分布在多个客户端。我们假设有N个客户端,客户端\(i\)的数据集为\(D_i\),那么这个客户端的局部损失函数定义为: \[ G_i(w,D_i)=\frac{1}{|D|}\sum_{\xi\in D_i}f(w,\xi) \] 其中\(w\)表示模型参数,\(D_i\)表示局部数据集的大小,\(\xi\)表示特定的数据样本,\(f\)为损失函数。联邦学习的目标是训练一个使全局损失函数最小化的模型即 \[ minF(w)=min\sum_{i=1}^{N}p_iF_i(w,D_i) \] \(p_i\)表示每一个客户端的权重,一般根据该客户端数据集大小占据总共数据集的多少
FedAvg由多次全局迭代组成,在每一次迭代\(t\)中,参数服务器将随机选择\(K\)个客户端作为\(K_t\),选择的客户端将从服务器端下载最新的模型\(w_t\),之后在每一个客户端上进行局部迭代,每一个epoch的梯度下降如下所示。 \[ w_{t+1}^{i}=w_t^i-\eta \nabla F_i(w_t^i,B_t^i) \] \(B^i_t\)是客户端的数据集\(D_i\)中的一个小批量样本,之后将在局部进行\(E\)个局部epoch来对模型进行更新\(g_{t+E}^i=w_{t+E}^i-w_t^i\) \[ w_{t+E}=w_t+\sum p_ig_{t+E}^i \] 即在原始的全局模型中将每一个客户端的更新梯度进行相加。之后将客户端的模型更新为新的模型。
一般来说,全局模型只会在局部模型进行E的整数倍训练之后进行更新。\(t\in I=\{E,2E,3E\}\)
论文解读
解决问题
该文章解决的问题主要是:BFL面临的通信延迟长和训练效率低
这可以归结为:
- 在BFL中,所有的中间模型的更新都会广播给所有矿工来维护区块链
- 每个客户端需要下载所有中间模型进行更新,以便本地进行模型聚合
所以作者就希望可以减少中间模型更新的数量来提高BFL的通信效率,利用\(Top_K\)算法对每个局部模型进行压缩,来减轻通信负载
BCFL流程
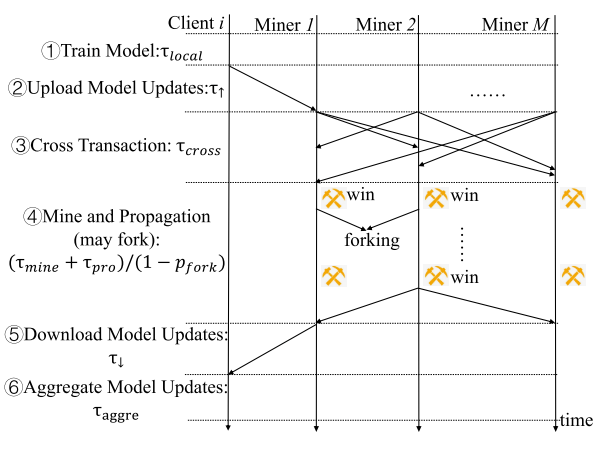
基础设定
区块链系统中有N个客户端,M个矿工。我们假设每一个客户端都连接着一个特定的矿工,这个矿工用来上传和下载模型的更新(但是一个矿工可以连接多个客户端)。在文章的系统中,使用的是TOPK算法和PoW的共识机制(这些可以进行更换)
主要步骤
本地模型训练
每个客户端使用梯度下降来更新本地的模型参数,更新公式如:\(w_{t+\frac{1}{2}}^{i}=w_t^i-\eta \nabla F_i(w_t^i,B_t^i)\),和传统FL一样,\(B\)是本地数据集中的一个batch,注意的是,这里并不是\(t+1\),而是\(t+\frac{1}{2}\) ,当且仅当在这次迭代之后需要上传模型时,才会令\(w_{t+1}^i=w^i_{t+\frac{1}{2}}\)。
我们将模型的更新定义\(g_{t}^i=w_{t+\frac{1}{2}}^i-w_{t+1-E}^i-m^i_{t+1-E}\)
这里和传统FL的区别就是,我们减去了一个\(m\),这个\(m\)就是补偿误差(去缓解压缩带来的误差)
\(Top_k\)算法其实就是设定一个阈值,如果模型更改的大小没有超过这个阈值,我们就认为这次更改并不是一个大更新,就不会将这次更新上传。

- 这里\(g^i_t\)是更新的梯度,其中应该有多个参数(和模型的维度\(d\)一样)
- 这里的阈值\(\phi\)就是这\(d\)个更新梯度中的第\(k+1\)个,也就是说,在这\(d\)个维度数据中,我们只取其前\(k\)大个数据,其他维度的国内新能数据设置为0。
模型上传
假设模型的维度是\(d\)(每一个维度对应一个更新梯度)每个维度更新的通信量为\(s\)字节
在BFCL中,k个模型上传所需要上传的字节为:\(k(s+\frac{log_2d}{8})\),传统的模型需要上传\(ds\)字节
\(k\)是我们选择的更新最大的\(k\)个维度,每个维度是\(s\)字节,剩下的一项是其索引的字节数。
中间相差的误差由\(m\)来弥补。
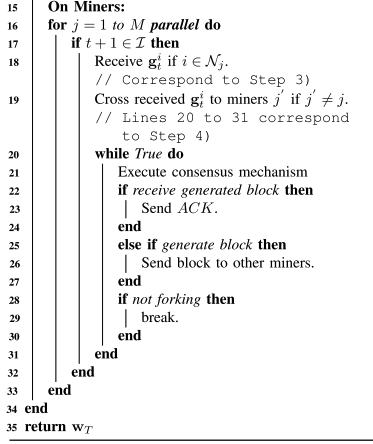
跨事务
在这一步骤中,客户端上传的所有模型更新都将存储在候选块中,之后每一个矿工(连接着一个服务器)将其服务器上的模型更新分发给其他矿工。这样所有矿工都会拥有全部节点的模型更新参数。
每一个矿工收取数据所需要的时间: \[ T_{cross,j}=\frac{(N-N_j)k(s+\frac{log_2d}{8})}{u_j} \]
- \(N-N_j\)代表有多少个服务器没有连接到矿工\(j\)上
- \(u_j\)就是下载速率
- 上式:除去连接到矿工上的服务器,矿工需要下载其他所有服务器的更新数据,更新数据大小为2中定义
挖矿和广播
在这一步骤中,每个矿工尝试生成一个区块(挖矿)来将客户端的所有模型更新存储到区块链上。所需要的时间是挖矿时间和传播时间。
Fork:
在有一个矿工挖矿成功过后,要将区块进行广播,在广播的期间,如果别的矿工也挖矿成功,就会出现fork情况。
- 挖矿时间:如果使用POW进行共识,挖矿过程的时间是不好进行确定的,所以只可以通过调整哈希难度来获得期望值,\(T_{mine}=E[x_{mine}]=\frac{1}{\lambda}\)
- 传播时间:传播的数据量为:\(\Omega=Nk(s+\frac{log_2d}{8})\),每个client生成的梯度大小。
- 总的时间:\(T=\frac{1}{\lambda}+max_{j\in M/j_w}\frac{\Omega}{u_j}\),\(M/j_w\)为除去挖到框的那个矿工。
如果在这个过程中,出现了fork现象,那么这个过程将会重新开始。为了避免分叉,矿工\(j_w\)的信息必须在矿工\(j\)挖到矿之前到达\(j\)。即:\(x_{mine,j}-x_{mine,j_w}>\frac{\Omega}{u_j}\)
所以分叉的可能性为:\(p_{fork}=1-\prod_{j\in M/j_w}Pr(x_{mine,j}-x_{mine,j_w}>\frac{\Omega}{u_j})\)

最终得出的运行时间为:

模型下载
获胜的矿工将成功生成一个区块,所有的客户端都需要从区块链上下载最新的区块来更新自己的训练模型。
下载时间:\(T_{\downarrow,i}=\frac{\Omega}{u_{\downarrow,i}}\)
模型聚合
一旦客户端获取到了最新的区块,他们就可以聚合模型更新来获得模型参数。
那么其最终消耗的时间为: \[ h(k,\lambda)=T_{local}+T_{aggre}+maxT_{\uparrow,i}+maxT_{cross,j}+(T_{mine}+T_{pro})/(1-p_{fork})+maxT_{\downarrow,i} \]
Remark 1:
假设一开始每个client和矿工的计算和通信能力是可以预测的,所以在给定\(\Omega\)的情况,是可以估算出\(h(k,\lambda)\)
Remark 2:
总时间受业务量\(\Omega\)的影响很大,如果k较少,那么较小的业务量会有效降低开销

收敛性证明
之后会补上的,这块真没看明白……o(╥﹏╥)o
结果分析
Comparison of Model Accuracy:
我们分别在CIFAR-10和FEMNIST上比较了BCFL与固定训练时间跨度500s和400s内的baseline的模型精度

- 在BFL中压缩模型更新可以有效提高训练效率。只要k是比d小得多的任意数字,在所有实验场景下,BCFL都可以实现比BFL高得多的模型精度。原因是BFL中沉重的通信负载消耗了过多的训练时间。
- 在BCFL中设置k和 λ ,模型的效果比其他所有的效果都要好
- 因为FEMNIST的维度很高,因此需要更多的全局迭代来训练有效的模型。在给定的时间跨度中训练的模型对于没有压缩的BFL而言性能不佳
Comparison of Model Accuracy with Fixed λ:
在BCFL中,λ 是控制块生成速率的参数。可以将 λ 固定为任意数字以控制块生成速率。

- BCFL的模型精度始终优于所有其他基线。
- 注意,在非IID CIFAR-10情况下BCFL的改进不如先前实验中的显著。原因是 λ 是一个固定的数字,没有分配其最优值。
Varying Compression Rates:

- x轴表示压缩率,y轴表示训练时间后的最终模型精度
- 文章的理论最佳设置可以在所有压缩率的基线中实现最高的最终模型精度。
Comparison of Training Time Consumption:
文章将目标模型精度分别固定为61%,58% 和82%,比较了每种算法的训练时间以达到目标模型精度


- BCFL算法总能以最短的训练时间达到目标最终模型精度。尽管BCFL可能不是通信流量最少的一个,但它需要较少的全局迭代来完成模型训练,从而使总训练时间成本最小化。更重要的是,与BFL相比,BCFL可以将消耗的训练时间减少90% 以上。
Varying Client and Miner Population:
通过将客户端和矿工的数量分别设置为\(N = M = 20、30、40、50\)来改变系统规模,以研究系统规模对模型精度性能的影响。同时,为了评估BCFL的鲁棒性,我们通过假设每个客户端在每次全局迭代中由于网络状况的突然变化 (例如网络拥塞或故障) 而没有返回模型更新的10% 概率来考虑网络的动态性。

- 即使网络是动态的,偶尔有离线客户端,BCFL仍然可以实现比BFL更高的模型训练性能。
- 随着客户端数量的增加,前两种情况下BCFL的模型精度会更高。原因在于更多的客户端可以为系统带来更多的计算能力。随着分配给每个客户端的样本数量减少,客户端可以更快地完成本地迭代。因此,通过在固定的训练时间范围内进行更多的全局迭代,可以提高最终模型的准确性。
- 在使用FEMNIST进行的实验中,无法观察到BCFL的模型准确性随客户群体的增加而增加。原因是每个客户的样本总体随着客户总体的增加而保持不变,从而无法减少本地培训时间。
- BFL的模型准确性随着客户人数的增加而变差。原因是BFL不能有效地禁止通信流量的增加。随着更多的客户端驻留在系统中,会产生更多的通信流量,这会严重延长通信时间,从而最终导致较低的模型精度。