本博客为在2023.07.01 - 2023.09.01期间阅读的10余篇论文笔记。
主题为:联邦学习、异构性、异步联邦学习、分层联邦学习
文章大体上来自于A、B会和A刊,少数几篇与GLOBECOM相似的出处不限。
(Skim)Asynchronous Hierarchical Federated Learning
Wang, Xing, and Yijun Wang. "Asynchronous hierarchical federated learning." arXiv preprint arXiv:2206.00054 (2022).
本文提出了一种异步的分层联邦学习,创新点为:
- 利用网络拓扑或聚类算法进行分组;
- 采用异步联邦学习容忍异构性。
👀主要解决同步分层联邦学习速度慢。
在联邦学习聚合的时候,每一个群组的leader会有一个队列,这个队列会存储来自每个客户机的参数,周期性地将结果聚合,不用等待一些掉队者的结果。并且作者提出,模型参数越过时,误差越大。因此文章采用了一个过时函数来控制每个客户机参数的影响程度。 \[ \alpha_{t'}=\alpha \times \sigma(t'-t) \] 这里\(\sigma\)是一个单调递减的函数用来控制影响程度。\(t'\)为聚合器收到中央服务器下发的最新模型的时间,那些尚未没有被聚合,仍然在队列中的模型参数的时间戳为\(t\),所以\(t'>t\)是一定成立的,而\(t\)越小,说明这个模型参数越过时,所以\(\sigma\)来降低其权重。
在中央服务器上,也有一个队列来存储聚合器的更新,由于异步学习,那么每个聚合器接收到的客户机的更新个数也不一样,所以聚合器上传要将聚合次数\(n_k\)、模型参数和时间戳\(t'\)一起上传。文章假设最新的全局模型的时间戳为\(t''\),\(t'' > t'\)。和上一层一样,中心聚合器也利用\(\sigma\)来权衡每个聚合器的权重,不同的是,聚合器接受的更新个数越多,也会相应提升其贡献。 \[ \alpha_{t''}=\frac{n_k}{N}\sigma(t''-t')\alpha \] 其中\(N\)为所有的客户机的总数。

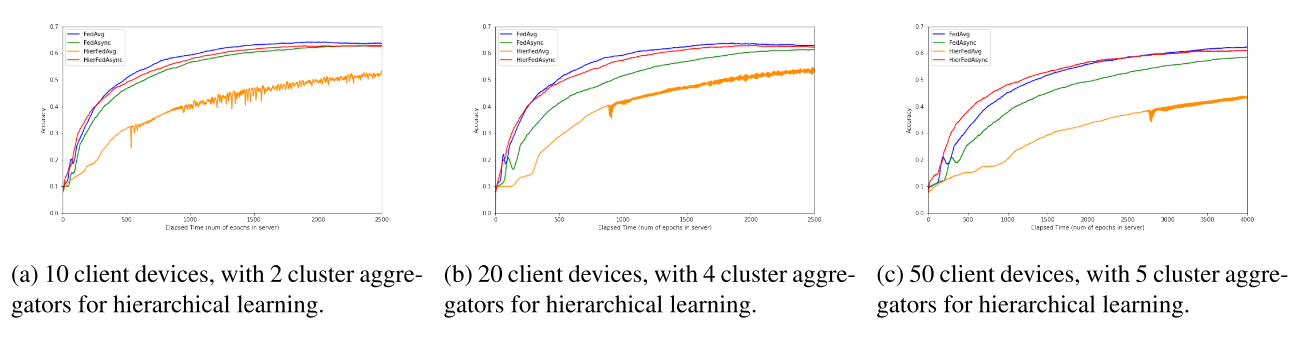
从结果来看,分层会大大增加学习系统的复杂性,使其收敛速度慢并且不稳定(橙色)。但是文章提出的异步操作缓解了分层的速度慢和稳定性差的问题。并且随着设备数的不断上升,文章的方法(红色)的优势更加明显。
不过另一层面:文章还统计了通信次数,也可以看出来分层其实是很显著地减少中心聚合器的负担。

对于本文的未来研究方向,有几个有趣的方向可以追求。首先,正如作者在论文中提到的,作者的加权机制偏向于对于计算和通信速度更快的设备进行学习,这在数据在客户端上是独立同分布(i.i.d.)的情况下效果很好。如果涉及到非独立同分布(non-i.i.d.)的数据,作者需要设计一个更复杂的加权机制来适应异步联邦学习。第二个有趣的研究方向是修改本地客户端学习中的简单L2正则化方法。作者还需要完成理论分析的推导和证明。
(Skim)WSCC: A weight-similarity-based client clustering approach for non-IID federated learning
Tian, Pu, et al. "WSCC: A weight-similarity-based client clustering approach for non-IID federated learning." IEEE Internet of Things Journal 9.20 (2022): 20243-20256.
本文提出了一种基于权重相似度的非iid联邦学习客户端聚类方法,创新点:
- 利用余弦距离度量来确定客户端集群;
- 不产生格外数据的情况下优化了通信开销。
👀主要就是为了解决non-iid的问题
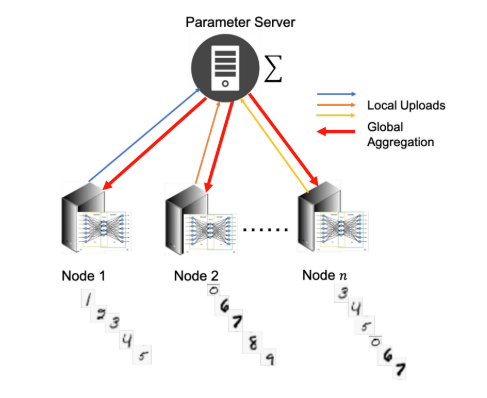
非IID类型:
- 标签分布:在这种情况下,节点之间的标签比例并不均匀分布。例如,一个节点可能具有某些标签的较高比例,而其他节点上可能没有出现某些标签。
- 特征不平衡:这指的是具有相同标签的样本具有不同特征,或者反过来。例如,在手写识别任务中,同一个数字可能有不同来源采集的各种特征。
- 数据集规模差异:当不同传感器收集的数据量大小不平等时,就会出现这种情况。样本较少的节点容易受到影响。
目前的问题是在联邦学习开始时候,各个节点的初始DNN模型是相同的,经过训练之后,如果仍然利用加权平均聚合,没有办法反应非IID的实际全局权重。
因此在非IID情况下,不能把目标函数定义为最小化加权平均的损失函数。而是应该保证每个节点都找到最小化的损失函数。 \[ w_i^*=argmin_{w_i}\{F_i(w_i)\} \] 为了解决这个问题,文章根据数据集的分布将一个联邦学习任务分解成多个同时进行的联邦学习任务,每个集群内部仍然使用IID模型,并用FedAvg协作。


在客户端层面:每个节点的初始模型参数是相同的,但是由于其各自的数据都是非IID的,所以在训练的时候,梯度也会发散,就如同下图一样。每个不同颜色的箭头代表一个分布。相似分布的梯度方向很可能会接近收敛。因此,在这项工作中,作者将联邦学习训练中的非独立同分布问题视为通过它们的分布对客户端进行聚类,并在同一聚类中聚合权重。
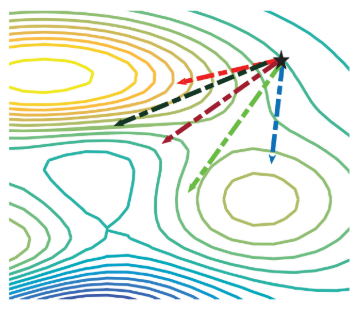
这里使用余弦相似性的原因为:余弦相似性不受到缩放效应的影响,特别是对于DNN模型的高维权重向量。
在每一轮聚合中,作者随机选择一个接收到的参数作为基准,用于计算余弦距离。然后使用距离向量作为后续聚类过程的输入(第5行)
这里文章中使用了AP聚类算法,具体可以见ChatGPT。对于非独立同分布物联网联邦学习任务,自适应聚类(AP)方法是理想的解决方案,因为它可以自动确定聚类数量。对于存在不确定节点的联邦学习任务,节点分布是未知的。
在节点层面:
这里有一个验证的阶段,节点将会对下发的全局模型进行验证,如果这个模型的准确性与节点内的本地模型的准确性低的程度大于阈值,就放弃该全局模型,继续使用原模型计算。
(CVPR)Learn from Others and Be Yourself in Heterogeneous Federated Learning
Huang, Wenke, Mang Ye, and Bo Du. "Learn from others and be yourself in heterogeneous federated learning." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
本文提出了一种联邦互相关和连续学习 FCCL(Federated Cross-Correlation and Continual Learning),创新点:
- 通过利用未标记的公共数据和自我监督学习来实现异构模型的泛化表示;
- 通过使用更新后的模型和预训练模型进行跨领域和内部领域的知识蒸馏,平衡来自其他模型和自身模型的知识。
👀本文解决的主要问题:1. 怎么在异构的联邦学习中学习到一种泛化表示,可以减轻漂移的问题;2. 怎么平衡多种知识来减少灾难性的遗忘(在本地训练的时候过拟合当前知识而忘记之前的知识),在域间或域内都能表现较好的性能。
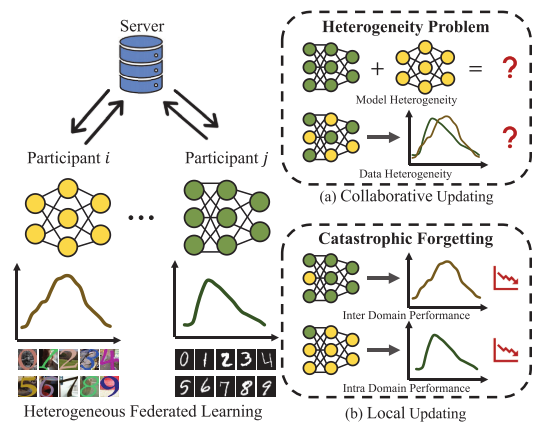
方法
这个文章总体上提出了两种不同的学习架构:联邦交叉相关学习(Federated Cross-Correlation Learning)、联邦持续学习(Federated Continual Learning)
联邦交叉相关学习
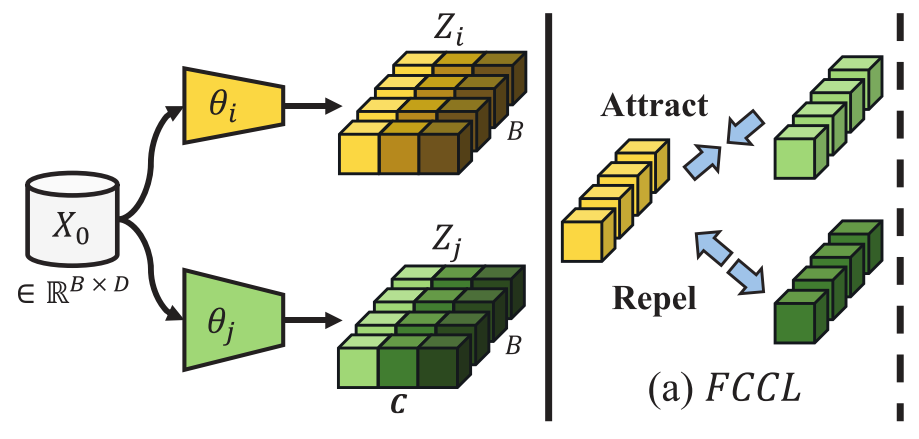
这个方法受到了自监督学习的启发,自监督学习可以获得一个比较泛化的模型。但是在这个工作中,由于异构的数据,导致相同标签的特征是有明显差异的,所以对于模型来说需要鼓励相同类别特征的不变性和不同类别特征的多样性。同时不同的模型承载不同的数据,这个数据是具有隐私性的,不适合自监督学习,为了保证安全,文章利用了无标签的公共数据。
通过自监督学习,增加不同类别之间的多样性和相同类别的不变性来学习一个泛化的模型。这样的表示能够尽可能地保留关于图像的信息,并在不同领域中具有一定的不变性。
文章构建了一种交叉相关矩阵:对于每个模型的logit输出为\(Z_i\),\(\bar{Z}=\frac{1}{K}\sum_iZ_i\)。计算第\(i\)个参与者的交叉相关矩阵: \[ M_i^{uv}=\frac{\sum_b||Z_i^{b,u}||\space||\overline{Z}^{b,v}||}{\sqrt{\sum_b||Z_i^{b,u}||^2}\sqrt{\sum_b||\overline{Z}^{b,v}||^2}} \] 其中\(b\)是批处理样本,\(u,v\)均表示logits层的维度索引。\(||·||\)是沿着批维度的归一化操作。最终得到\(M_i\)是一个维度为\(C\)的方阵,其中数据介于-1到1(不相似到相似)。协作的loss值设置为 \[ L_i^{Col}=\sum_{u}(1-M^{uu})^2+\lambda_{Col}\sum_{u}\sum_{v\neq u}(1+M_{i}^{uv})^2 \] \(\lambda_{Col}\)用来权衡两项的重要性,当交叉相关矩阵的对角线元素取值+1时,它鼓励来自不同参与者的logits输出相似;当交叉相关矩阵的非对角线元素取值-1时,它鼓励logits输出的多样性,因为这些logits输出的不同维度将彼此不相关。
联邦持续学习
传统的监督损失函数会引发两个问题:1. 在局部更新中,由于没有其他参与者的监督,模型容易过拟合当前数据分布;2. 目标设计通常只根据先验概率独立地对预测结果进行惩罚,这提供了有限且较为僵硬的领域内信息。
因此文章中提出了一种兼顾领域内和领域间的知识蒸馏方法。
在每次中央服务器下发模型之后,每个参与者会获得一个\(\theta_i^{t-1}\),这个模型是通过全局聚合得到的,所以拥有其他参与者学到的知识。
那么组间的知识蒸馏loss就为 \[ L_i^{Inter}=\sigma(Z_{i,pvt}^{t-1})log\frac{\sigma(Z_{i,pvt}^{t-1})}{\sigma(Z_{i,pvt}^{t,im})} \] 目的是在保持隐私的同时,不断向他人学习,来保证域间的性能,缓解联邦学习中的灾难性遗忘。
此外对于第\(i\)个参与者,作者可以使其在自己的私有数据上对模型进行预训练获得\(\theta_i^*\),然后利用其的logit输出\(Z_{i,pvt}^*\)来对域内进行知识蒸馏: \[ L_i^{Intra}=\sigma(Z_{i,pvt}^*)log\frac{\sigma(Z_{i,pvt}^*)}{\sigma(Z_{i,pvt}^{t,im})} \] 在一定程度上,上述的两个模型分别代表了域间的老师模型和域内的老师模型(\(\theta_i^{t-1}\),\(\theta_i^*\))
所以最后双向知识蒸馏的loss为两者相加。 \[ L_i^{Dual}=L_i^{Inter}+L_i^{Intra} \] 联邦持续学习的整体loss为: \[ L_i^{Loc}=L_i^{CE}+\lambda_{Loc}L_i^{Dual} \] \(L_i^{CE}\)为传统的交叉熵损失。
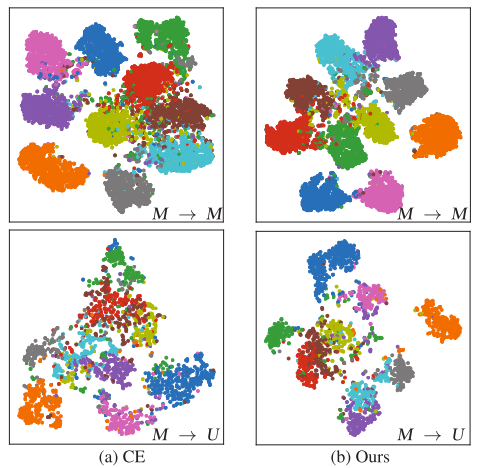
利用双向知识蒸馏学习到的特征在领域内和领域间都更加紧凑且分离。模型展现出更好的区分特征,产生了有前景的领域内和领域间性能。

(CVPR)FedDC: Federated Learning with Non-IID Data via Local Drift Decoupling and Correction
Gao, Liang, et al. "Feddc: Federated learning with non-iid data via local drift decoupling and correction." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2022.
作者提出了一种新的局部漂移解耦与修正的联邦学习算法(FedDC),创新点为:
- 动态更新每个客户端的局部目标函数(1. 约束惩罚项:表示全局参数、漂移变量和局部参数之间的关系;2. 梯度修正项:减少每一轮训练中的梯度漂移);
- 在训练过程中通过引入漂移变量对局部模型和全局模型进行解耦,减小了局部漂移对全局目标的影响,使其收敛速度更快,达到更好的性能。
👀本文解决的主要问题就是联邦学习中的客户端漂移问题
在异构的联邦学习中,客户端的局部最优点和全局最优点是不一致的。
客户端漂移
每个客户端在本地数据集上训练的本地模型和直接在全局数据集上训练的全局模型之间存在漂移,如果忽略漂移,服务器将无法得到较好的模型,而非IID数据是高度倾斜的,所以普通的FedAvg性能会明显降低。
举个简单的例子:
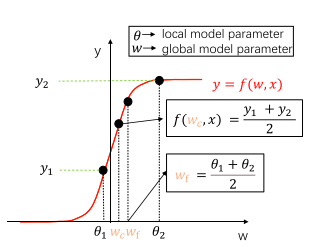
假设模型中存在一个 非线性的 变换函数\(f\),\(\theta_1\)和\(\theta_2\)是两个客户端的局部参数,\(w_c\)为理想的模型参数,\(w_f\)是FedAvg获得的参数。客户端的漂移用\(h\)表示,那么\(h_1 = w_c-\theta_1\),\(h_2=w_c-\theta_2\)。\(x\)是一个数据点,那么客户端1对应的输出应该是\(y_1=f(\theta_1, x)\),同样的客户端2的输出为:\(y_2=f(\theta_2, x)\)。利用FedAvg获得的模型参数\(w_f=\frac{\theta_1+\theta_2}{2}\),而理想的模型参数应该为\(w_c=f^{-1}(\frac{y_1+y_2}{2})/x\),因为\(f\)不是一个线性函数,所以\(w_c\neq w_f\),\(f(w_f,x)\neq\frac{y_1+y_2}{2}\)。
这就说明FedAvg的全局模型是漂移的,因此本文章要学习全局和局部模型之间的局部漂移,并在将局部模型参数上传到服务器之间将局部漂移桥接起来。
方法
优化目标与参数更新
首先,文章为每个客户端定义了一个局部漂移变量\(h_i\),在理想的情况下,局部漂移变量应该为\(h_i=w-\theta_i\),这里\(w\)为全局模型参数,\(\theta_i\)是客户端\(i\)的局部模型参数。在训练过程中,需要保持这个限制,所以作者将其作为惩罚项 \[ R_i(\theta_i, h_i,w)=||h_i+\theta_i-w||^2 \] 通过引入\(R\),作者将方程约束优化,变成无约束优化问题。
最后的目标函数为 \[ F(\theta_i,h_i,D_i,w)=L_i(\theta_i)+\frac{\alpha}{2}R_i(\theta_i, h_i,w)+G_i(\theta_i,g_i,g) \] 其中,\(L\)是经验损失函数,\(G\)是梯度修正项(\(G_i(\theta_i,g_i,g)=\frac{1}{\eta K}<\theta_1,g_i-g>\),其中\(\eta\)是学习率,\(K\)是一轮训练的迭代次数,\(g_i\)是客户端i上一轮本地参数的更新值,\(g\)是所有客户端上一轮本地参数的平均更新值。在第t轮,\(g_i=\theta_i^t-\theta_i^{t-1},g=E_{i\in[N]}g_i\),其作用是减少局部梯度的方差。 \[ \theta_i^{t,k+1}=\theta_i^{t,k}-\eta\frac{\partial F(\theta_i^{t,k},h_i^t,D_i,w^t)}{\partial \theta_i^{t,k}} \] 👆🏻这个是在第t轮的第k个局部训练迭代中,局部模型参数更新方程,这个方程会在一轮中运行K次。
Que:
在FedDC中,其penalized term R和gradient correction term G的区别是什么,其引用的SCAFFOLD中的梯度修正项就是为了缓解drift,为什么在FedDC中又引入了penalized term 去减少drift?
Ans:
当涉及到联邦学习中的漂移问题时,特别是客户端漂移,不同的方法可能会采取不同的策略来缓解漂移并提高模型的稳定性。以下是关于在 FedDC 中的 penalized term R 和引用的 SCAFFOLD 中的 gradient correction term G 的更详细的解释以及它们在处理漂移时的不同机制:
Penalized Term R(在 FedDC 中):
Penalized term R 是一种正则化项,被添加到客户端模型的损失函数中。它的目的是在更新客户端模型的参数时,通过惩罚大幅度变化的参数,使得客户端模型的参数更加趋于全局模型。这种方式类似于在损失函数中添加权重衰减(weight decay)或 L2 正则化项,从而阻止模型参数过度拟合训练数据。在联邦学习中,由于每个客户端的本地数据分布和规模可能不同,导致模型的漂移,特别是在训练初期。通过添加 penalized term R,可以促使客户端模型的参数更加接近全局模型,从而在一定程度上减轻客户端漂移问题。
Gradient Correction Term G(在 SCAFFOLD 中):
Gradient correction term G 是引用自 SCAFFOLD 论文的一种方法,它的目标是在客户端训练过程中调整梯度更新,以减少模型的漂移。具体而言,SCAFFOLD 引入了一种梯度校正项,该项对每个客户端的梯度进行调整,使得每个客户端更新更加平稳,从而减少漂移的影响。这种方式可以看作是在梯度下降的过程中,对每个客户端的梯度更新进行微调,以提高模型的稳定性。
举个例子来说明这两种方法的不同作用方式:
假设有一个联邦学习任务,涉及多个医院的病人数据,每个医院都有不同的数据分布和疾病情况。客户端漂移问题可能导致某些医院的模型在某些轮次训练后出现不稳定的性能下降。在这种情况下:
- Penalized Term R(在 FedDC 中): 在 FedDC 中,通过在客户端模型的损失函数中添加 penalized term R,可以约束每个客户端的参数变化,使得客户端的模型更接近于全局模型。这样一来,即使某些客户端的数据分布有所不同,它们的模型参数变化也会受到一定的限制,从而减轻漂移问题。
- Gradient Correction Term G(在 SCAFFOLD 中): 在 SCAFFOLD 中,gradient correction term G 会调整每个客户端的梯度更新,使得每个客户端的模型更新更平稳。这种方式不仅仅是通过参数惩罚,还直接在梯度更新阶段对漂移进行修正,从而减少模型的不稳定性。
Que:
但是不太一样的是SCAFFOLD论文将G放到了最后的聚合步骤中,但是在FedDC中,其将G放到了损失函数(或者叫目标函数)中,这为什么不同了?
Ans:
在不同的联邦学习方法中,关于如何处理模型的漂移问题以及何时引入修正项的具体策略可能会因方法的设计和目标而有所不同。在 SCAFFOLD 和 FedDC 中,虽然都涉及到模型漂移问题的解决,但在具体的实现方式上有所差异。下面我会详细解释这两种方法中为什么会有这样的不同设计。
SCAFFOLD:
在 SCAFFOLD 中,作者引入了梯度修正项 G,该项是在最后的模型聚合阶段应用的。这种方式的优势在于,通过在模型聚合时对梯度进行修正,可以在整个联邦学习过程中减少模型的漂移。由于模型聚合是最后一步,这样的修正可以确保每个客户端的模型都在全局更新中起到一定的平衡作用。
FedDC:
在 FedDC 中,将梯度修正项 G 放入损失函数(或目标函数)中,是为了在客户端的本地训练过程中对梯度进行修正。这种设计可以使每个客户端在本地训练阶段就能够对模型的漂移问题进行处理,而不仅仅是依赖于模型的聚合过程。在每个客户端的损失函数中引入梯度修正项 G,可以在本地训练时即时地修正模型,以适应当前的数据分布和特点。
综上所述,这两种方法之间的不同设计是因为它们在解决漂移问题时的侧重点和策略不同。SCAFFOLD 更侧重于在模型聚合时对漂移进行修正,而 FedDC 则更侧重于在每个客户端的本地训练过程中就开始处理漂移。
对于局部漂移参数的更新,如果假设局部参数不变,那么更新公式应该是\(h_i^+=h_i+(w^+-w)\),这里的\(+\)表示新参数。但是由于全局数据不可用,不可能直接获得全局的最新参数。
因此作者利用\(\theta_i\)来代替\(w\),这是因为在每轮开始,都会有\(\theta_i=w\);利用\(\theta_i^+\)代替\(w^+\),因为\(\theta_i^+\)是对\(w^+\)的估计。 \[ h_i^+=h_i+(w^+-w) \approx h_i+(\theta^+_i-\theta_i) \] 那么局部模型的参数更新就可以将局部漂移参数引入来减少漂移问题,即\(\theta_i^++h_i^+\),所以聚合方程变成了: \[ w^+=\sum_{i=1}^N\frac{D_i}{D}(\theta_i^++h_i^+) \]
讨论
该文章与SCAFFOLD不同的点在于:SCAFFOLD是限制局部优化方向以减小局部模型与全局模型之间的参数差距,即限制\(\theta_i\)接近\(w\)(即\(min||\theta_i−w||\))。然而,限制局部模型的优化方向阻碍了它在拟合局部数据集分布,因为局部分布和全局分布可能是不一致的。在FedDC中,文章认为学习参数间隙比限制它更好。FedDC利用局部漂移变量来学习局部模型和全局模型之间的参数差距。然后利用局部漂移变量来弥合差距,在这里我们学习局部漂移\(h_i\)来实现目标\(min||\theta_i + h_i − w||\)。
(CVPR)Fine-tuning Global Model via Data-Free Knowledge Distillation for Non-IID Federated Learning
Zhang, Lin, et al. "Fine-tuning global model via data-free knowledge distillation for non-iid federated learning." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2022.
文章提出了一种无需数据的知识蒸馏方法来调整服务器中的全局模型(FedFTG),创新点:
- 通过无数据蒸馏对服务器中的全局模型进行微调,充分利用了服务器的计算能力;
- 开发了硬样本挖掘来有效地将知识转移到全局模型;提出了定制的标签采样和类级集成,以方便最大限度地利用知识;
- 证明了FedFTG与现有的本地优化器是正交的,可以当做插件来使用。
👀文章解决的问题是:联邦学习中非IID的问题,具体来说是非独立同分布的数据会导致:局部模型漂移、灾难性遗忘全局知识。
现在大多数方法,包括上文的SCAFFOLD都是对局部模型的更新方向进行约束,使得局部和全局优化目标保持一致。但是SCAFFOLD只通过简单的模型聚合来获取服务器中的全局知识,忽略了局部知识的不兼容性,导致全局的知识遗忘。
方法
基于硬样本挖掘的无数据知识提取全局模型微调
在传统的联邦学习基础上,文章使用了一种无数据的知识蒸馏方法来对全局模型进行微调
服务器维护了一个条件生成器\(G\),它生成伪数据来捕获客户端的数据分布,如下所示: \[ \tilde{x}=G(z,y;\theta) \] 其中\(\theta\)是\(G\)的参数,\(z\sim N(0,1)\)是标准的高斯噪声,\(y\)是预定义分布\(p_t(y)\)采样的\(\tilde{x}\)的类标号。
全局模型要解决的目标函数是:
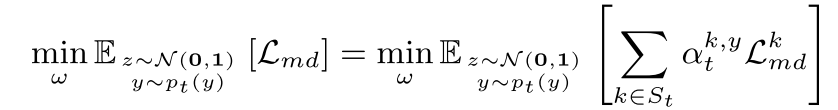
\(\mathcal{L}_{md}^k\)是全局模型\(\omega\)和本地模型\(\omega_k\)之间的模型差异:\(\mathcal{L}_{md}^k=D_{KL}(\sigma(D(\tilde{x};\omega))||\sigma(D(\tilde{x};\omega_k)))\),\(D\)是分类器,\(\sigma\)是全连接函数,用来输出\(\tilde{x}\)的预测分数,\(D_{KL}\)指的是Kullback-Leibler散度。通过最小化\(\mathcal{L}_{md}^k\)就可以使得\(\tilde{x}\)在全局模型上的结果和\(x\)在局部模型上的结果相似,即可以将局部模型中的知识转移到全局模型中。
生成伪数据:
为了更好地从局部模型中提取知识,伪数据\(\tilde{x}\)应该契合局部模型的输入空间,文章使用了语义损失\(\mathcal{L}_{cls}^k\)来训练生成器\(G\)。
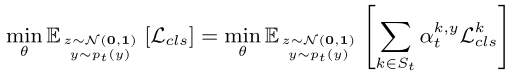
其中\(\mathcal{L}_{cls}^k\)是局部模型对伪数据\(\tilde{x}\)的预测与类别标签\(y\)之间的交叉熵损失:\(\mathcal{L}_{cls}^k=L_{CE}(\sigma(D(\tilde{x};\omega_k)),y)\),通过最小化该函数,\(\tilde{x}\)对\(y\)产生更高的预测,因此其更适合\(y\)类的数据分布。只使用生成器会为每个类产生相同的数据,为了解决这个问题,文章使用了多样性损失\(L_{dis}\)来提高数据的多样性。
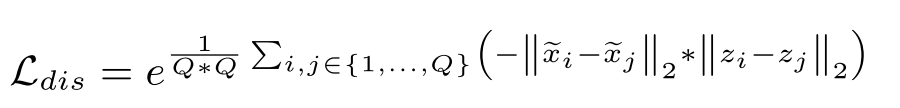
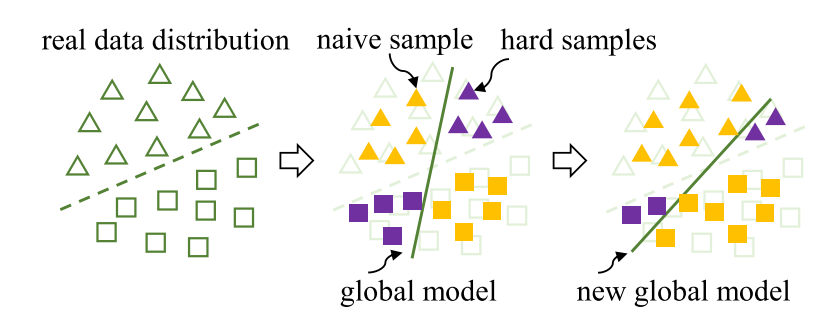
硬数据挖掘:
使用\(L_{cls}\)训练生成器\(G\)将生成具有低分类误差的伪数据\(\tilde{x}\),但是这种伪数据有着最容易被区分的特征,这种数据会很易于分类。然而,朴素的样本并不会导致全局模型和局部模型之间的观测不一致,\(L_{md}=0\)。所以为了有效地利用局部模型中的知识并将其转移到全局模型中,我们使用了全局模型和局部模型预测不一致的硬样本,具体来说:
- 强制生成器\(G\)生成最大化\(L_{md}\)的硬样本
- 使用硬样本训练全局模型来最小化\(L_{md}\)。
因此全局模型可以逐渐微调来适应数据分布:
适应标签分布变化实现有效知识蒸馏
对于数据异构的客户端,有以下两个问题
- 客户端的本地数据集是类不均衡的,\(D_k\)训练的本地模型包含不均衡的数据信息
- 对于一个类,知识的重要性在本地模型中是不同的。
为此,文章分别提出了自定义标签采样和类集成来适应这两个问题
自定义标签采样
在数据异构的情况下,本地数据是类不平衡的,会出现有些类甚至没有证据。已经证明了:深度神经网络倾向于学习多数类而忽略少数类。因此,局部模型的少数类的数据信息可能是错误和误导的,生成的伪数据对于度量模型差异是无效的。
为了缓解这个问题,文章根据每轮整个训练数据的分布自定义采样概率\(p_t(y)\) \[ p_t(y)\varpropto \sum_{k\in S_T}\sum_{i=1}^{N_k}E_{(x_k^i,y_k^i)\sim D_k}[1_{y_i=y}]=\sum_{k\in S_t}n^{y}_k \] 其中\(1_{condition}\)是\((condition == true)\),\(n_k^y\)是客户端\(k\)中\(y\)类的样本数量。这样,多数类的伪数据产生的概率较高。
类集成
知识蒸馏中广泛使用的集成方法为来自不同教师模型的知识分配相同的权重,即\(\alpha_t^{k,y}=\frac{1}{|S_t|}\)。
但是由于标签分布的变化,对于同一个类,不同的局部模型中知识的重要性是不同的,如果给每个客户端分配相同的权重,重要的知识就不能被正确的理解和利用。
因此,文章通过客户端\(k\)中的\(y\)类的数据相对于\(S_t\)的总数据的比例来计算\(\alpha_t^{k,y}\) \[ \alpha_t^{k,y}=n_k^y/\sum_{i\in S_t}n_i^y \]


局限性
该工作的主要局限性在于计算效率。由于FedFTG在本地训练的基础上增加了对全球模型的训练,因此使得整个训练的时间比其他方法要长。在我们的实验中,FedFTG在每一轮通信中所需的时间大约是FedAVG的两倍。
(CVPR)Layer-wised Model Aggregation for Personalized Federated Learning
Ma, Xiaosong, et al. "Layer-wised model aggregation for personalized federated learning." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2022.
本文提出了一种全新的pFL框架pFedLA,其可以实现联邦学习个性化的分层聚合,能够从客户端模型中准确地识别出每一层的效用。
面向的仍然是客户端的异构,现有的pFL在整个模型参数或不同客户端的损耗值之间应用距离度量,这不足以利用他们的异构性。可能导致不准确的权重组合或非IID分布式数据的贡献不平衡。
对于个性化联邦学习,文章发现了利用层间相似度进行聚合比起利用模型相似度进行聚合有更高的模型精度。
文章还说明了不同的层应用不同的权值,例如全连接层权重较高而卷积层权值较小可以产生显著的性能增益。
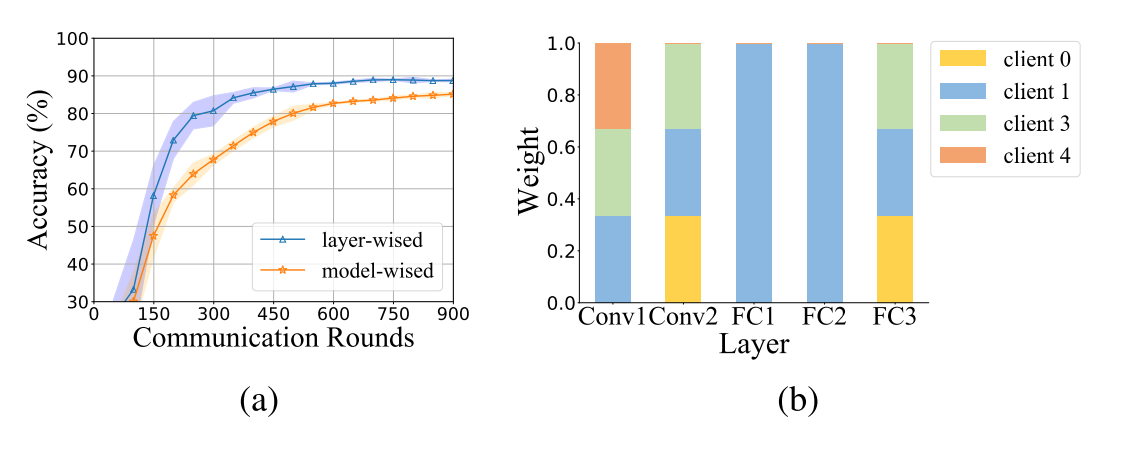
如今的pFL有两种不同的实现方法:
- 基于数据的方法:侧重于减少客户端数据集的统计异构性
- 基于模型的方法:侧重于为不同的客户生成定制的模型参数或结构
一般来说,为每个客户端生成有效的个性化参数引用 超网络 来实现
算法部分
pFedLA
pFedLA评估了来自不同客户端的每一层的重要性,以实现分层感知的个性化模型聚合。其在服务器上为每一个客户端应用一个专用的超网络,并训练他们为每个客户端的模型层生成聚合权重值。对于每一个客户端也有一个个个性化的模型。
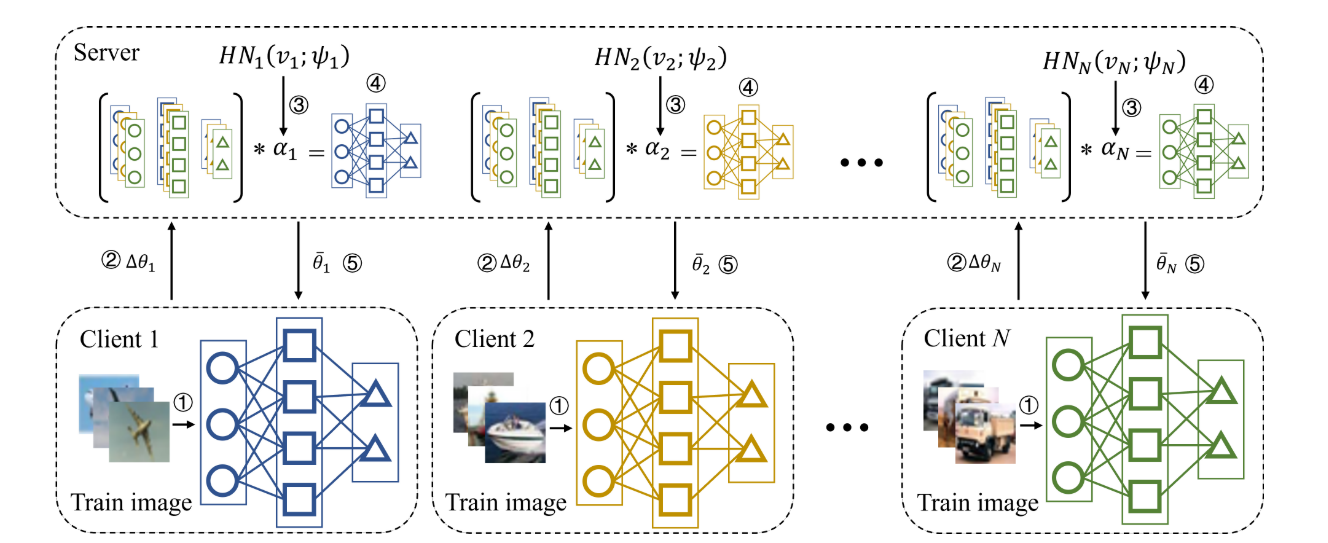
文章在服务器端应用了一组聚合权重矩阵\(\alpha_i\)来逐步利用客户端在层次上的相似性。

其中\(\alpha_i^{ln}\)表示客户端\(i\)中第\(n\)层的聚合权重向量,\(\alpha_i^{ln,N}\)表示剩余客户端\(N\)在客户端\(i\)第\(n\)层聚合的权重,对于所有的\(n\)个层,\(\sum_{i=1}^N\alpha_{i}^{ln,j}=1\)。
与其他的pFL不同,pFedLA不是对客户端模型的所有层应用相同的权重,而是考虑神经层的不同效用,为每个层分配不同的权重。
每个超网络由几个全连接层组成,输入是一个嵌入向量,该向量随模型参数自动更新,输出是\(\alpha\),定义为 \[ \alpha_i=HN_i(v_i;\psi_i) \] 其中\(v_i\)是嵌入向量,\(\psi_i\)是超网络的模型参数。设\(\{\theta^{l1},...,\theta^{ln}\}\)是本地训练后所有客户端中间参数,\(\theta^{ln}=\{\theta_1^{ln},...,\theta_n^{ln}\}\)是所有客户端的第\(n\)层的参数集合。在pFedLA中,模型的参数聚合如下: \[ \bar{\theta_i}=\{\bar{\theta_i}^{l1},\bar{\theta_i}^{l2},...,\bar{\theta_i}^{ln}\}=\{\theta^{l1},...,\theta^{ln}\} *\alpha_i \]
\[ \bar{\theta_i}^{ln}=\sum_{j=1}^N\theta_j^{ln}\alpha_i^{ln,j} \]
因此,pFedLA的目标函数为:
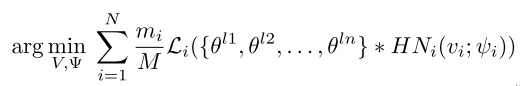

在每一轮通信中,客户端首先从服务器下载最新的个性化模型,然后使用本地SGD基于私有数据进行训练,之后每个客户端的模型更新\(\Delta\)将被上传到服务器用来更新\(v\)和\(\psi\)。
HeurpFedLA:通信效率的改进
通信开销主要来自于客户端传输的\(\Delta\theta_i\)和服务器发送的\(\bar{\theta}_i\)。
HeurpFedLA将启发地选择哪些层在本地保留,哪些层在全局进行聚合。其关键思想是:启发地选择具有高\(k(AT_K)\)的聚合权重去本地更新。具体来说,对于客户端\(i\)的所有层,利用聚合权重值:\(\alpha_i^{l1,i},...,\alpha_i^{ln,i}\)进行降序排序,并选择相应的最上面的\(k\)个层进行保留,并不上传。
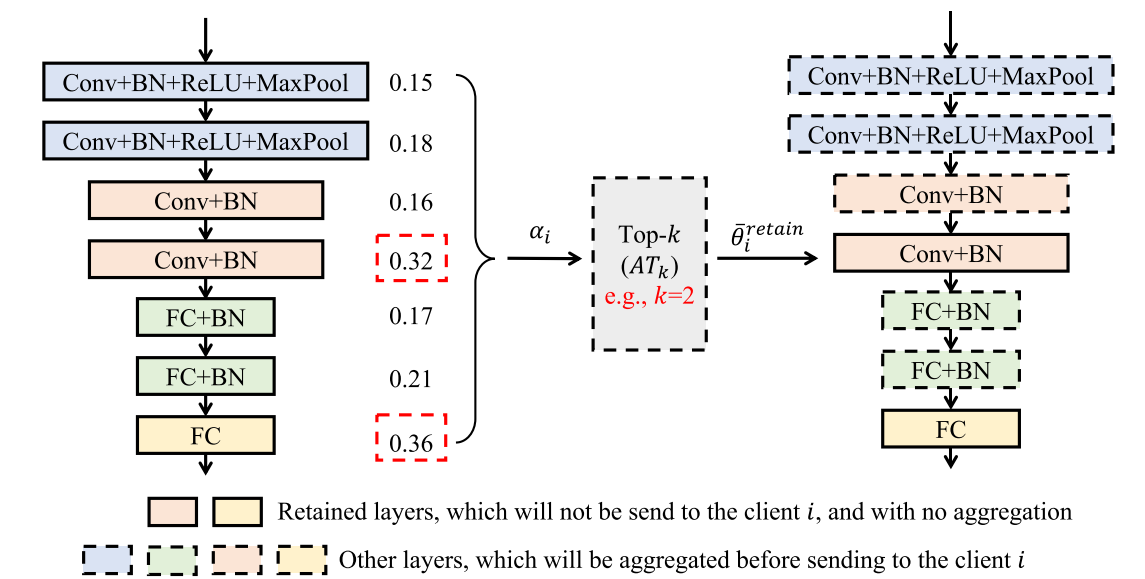
这个做法的原理是:等级越高的层对于模型个性化的贡献越大,这也意味直接在个性化模型中使用这些层对训练性能的影响很小。
(CVPR)Robust Federated Learning with Noisy and Heterogeneous Clients
Fang, Xiuwen, and Mang Ye. "Robust federated learning with noisy and heterogeneous clients." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
文章提出了一种鲁棒的异构联邦学习(RHFL),其可以同时处理噪声和执行联邦学习,创新点:
- 利用公共数据直接对齐模型反馈,不需要格外的共享全局模型进行协作
- 采用鲁棒的抗噪损失函数减少负面影响
- 设计了一种新的客户信心加权方案,在联邦学习阶段自适应为每个客户分配权重。
解决的问题是:模型异构性,以及不同客户端拥有不同的噪声
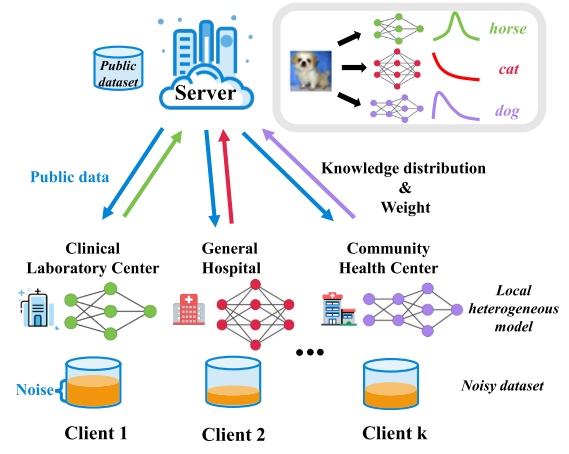
算法部分
问题阐述
- 在异构联邦学习设置下,文章考虑了\(K\)个客户端和一个服务器,\(C\)为客户端的集合,\(|C|=K\),客户端\(k\)拥有私有数据集\(D_k=\{(x_i^k,y_i^k)\}_{i=1}^{N_k}\),\(y\)用独热向量表示。
- 客户端拥有不同的神经架构\(\theta_k\),\(f(\cdot)\)表示神经网络,\(f(x^k,\theta_k)\)表示输入参数\(x^k\)的输出。因为服务端不能访问客户端,所以服务端拥有一个共享数据集\(D_0\)。
- 在异构联邦学习中,学习过程分为协作学习阶段和局部学习阶段,协作学习有\(T_c\)个epoch,局部学习有\(T_l\)个epoch。
- 文章假设每个客户端都有一个私有的噪声数据集\(\tilde{D}_k=\{(x_i^k,\tilde{y}_i^k)\}_{i=1}^{N_k}\),\(\tilde{y}_i^k\)表示噪声的标签,由于噪声模型也是异构的,\(f(x,\theta_{k_1})\neq f(x,\theta_{k_2})\)。因此,客户端除了自己本地数据集的噪声以外,还要关注其他客户端的噪声。
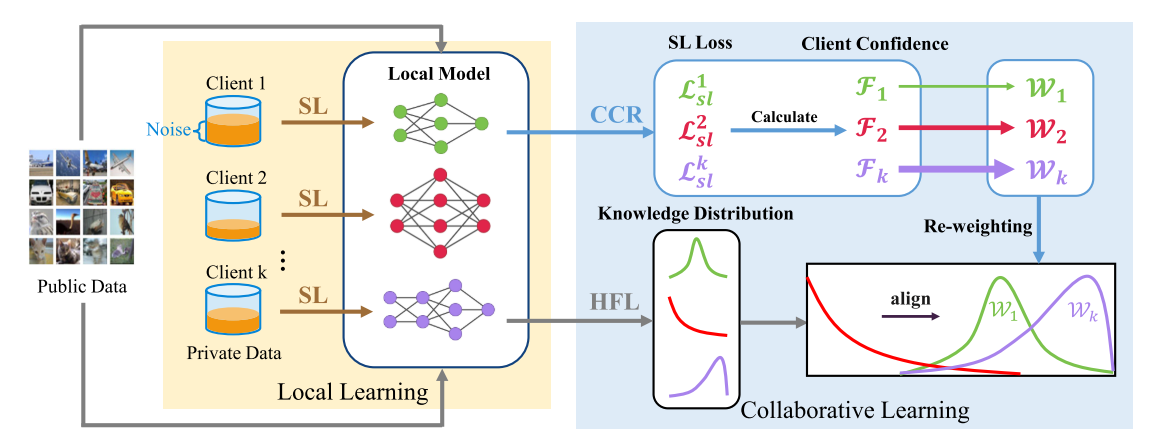
异构联邦学习
在联邦学习阶段,文章使用公共数据集\(D_0\)作为客户端之间沟通的桥梁,在协作学习时期,客户端\(c_k\)利用本地模型\(\theta_k^{t_c}\)在公共数据集上的输出来获得该客户端的知识分布\(R_k^{t_c}=f(D_0,\theta_k^{t_c})\)。客户端使用KL散度来衡量来自其他客户端的知识分布差异。 \[ KL(R_{k_1}^{t_c}||R_{k_2}^{t_c})=\sum R_{k_1}^{t_c}log(\frac{R_{k_1}^{t_c}}{R_{k_2}^{t_c}}) \] 两个客户端的知识分布差异越大,则两方可以相互学习的越多,因此最小化概率分布\(KL\)可以被认为是其中\(c_{k_1}\)向\(c_{k_2}\)学习的过程。 \[ \mathcal{L}_{kl}^{k,t_c}=\sum_{k_0=1,k_0\neq k}^KKL(R_{k_0}^{t_c}||R_{k}^{t_c}) \] 客户端通过调整知识分布来向他人学习
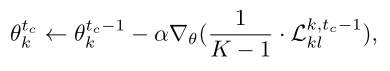
本地噪声学习
为了减少局部噪声的影响,文章参考了对称交叉熵学习中提到的方法。将\(p\)和\(q\)分别表示标签类分布和预测类分布,那么交叉熵损失应该为: \[ \mathcal{L}_{ce}=-\sum_{i=1}^Np(x_i)log(q(x_i)) \] 但是由于标签噪声的存在,单纯使用交叉熵损失不能使所有的类都被充分学习或正确分类所有类别,为了完全收敛难学的类,模型会执行更多轮的学习,这就使学习的类更倾向于过拟合嘈杂的标签,使模型整体性能下降。
一般来说,模型在一定程度上可以正确分类,并且由于噪声的存在,模型的预测结果甚至比标签更加可靠,所以\(p\)可能不是真实的类分布,反而\(q\)才是!
因此文章提出了基于\(q\)的损失函数反向交叉熵 \[ \mathcal{L}_{rce}=-\sum_{i=1}^Nq(x_i)log(p(x_i)) \] 通过结合CE损失以及RCE损失,模型可以完全学习难以学习的类,同时防止过拟合(CE损失增强了模型对各类别的拟合效果,RCE损失对标签噪声有鲁棒性) \[ \mathcal{L}_{sl}=\lambda\mathcal{L}_{ce}+\mathcal{L}_{rce} \] 在本地学习阶段,客户端将使用自己的本地数据集进行更新,以防止遗忘本地知识,在训练迭代过程中,标签噪声会导致模型往错误的方向更新,最终无法收敛。为了避免这个问题,文章采用SL损失来计算模型的损失,局部更新函数为
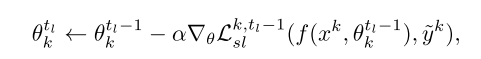
客户端信心重新加权(CCR)
文章提出了客户端的信心重新加权(CCR)的方法,以减少来自其他客户端的标签噪音在协作学习阶段的不利影响。CCR可以在通信过程中个性化每个客户端的权重,以减少噪声客户端的贡献,并更多地关注具有干净数据集和高效模型的客户端。
根据上文我们知道SL损失其实是代表了数据集的干净程度,SL越小表明这个数据集噪声越小,因此文章定义了数据集的质量:
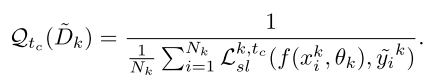
为了量化客户端的学习效率,我么你在每一轮迭代中计算SL的下降率,SL下降率越大说明其学习效率越高: \[ \mathcal{P}(\theta_k^{t_c})=\Delta\mathcal{L}_{sl}^{k,t_c}=L_{sl}^{k,t_c-1}-L_{sl}^{k,t_c} \] 那么在协作学习阶段中,同时考虑标签质量和学习效率,文章将循环\(t_c\)中的第\(k\)个客户端的信心定义为 \[ \mathcal{F}_k^{t_c}=\mathcal{Q}_{t_c}(\tilde{D}_k)\cdot\mathcal{P}(\theta_k^{t_c}) \] 最后的聚合权重为: \[ w_k^{t_c}=\frac{1}{K-1}+\eta\frac{\mathcal{F}_k^{t_c}}{\sum_{i=1}^K\mathcal{F}_k^{t_c}} \]
\[ \mathcal{W}_k^{t_c}=\frac{exp(w_k^{t_c})}{\sum_{k=1}^Kexp(w_k^{t_c})} \]
所以最后的协作学习阶段的聚合函数如下:
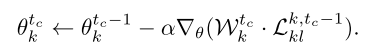
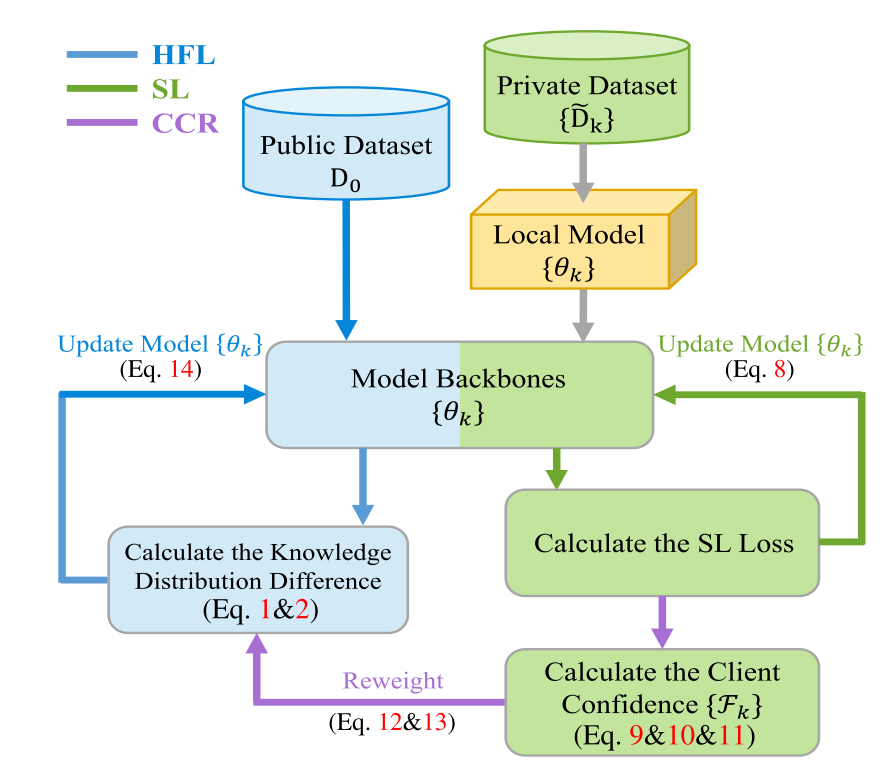
(CVPR)Local Learning Matters: Rethinking Data Heterogeneity in Federated Learning
Mendieta, Matias, et al. "Local learning matters: Rethinking data heterogeneity in federated learning." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
文章首先分析了正则化的方法在减轻数据异构性影响的表现是非常出色地。
文章其次提出了一种基于正则化并最大限度减少计算和内存开销的联邦学习方法 FedAlign
解决的问题是:模型异构性,减轻异构联邦学习导致的高额计算和内存开销
文章认为正则化技术是一个防止模型过拟合的技术,类似的,在FL中,本地设备在训练中过拟合对整体网络性能是有害的,因此可以提高本地模型的普遍性来使得客户端的目标更接近全局目标。
分析
文章比对了多种最先进的FL算法(经典baseline和最新技术:FedAvg, FedProx, Moon; 三种最先进的正则化方法:Mixup, Stochastic Depth, GradAug),发现了正则化的方法在异构的情况下更具有优势,文章进一步在基于二阶信息上进行了分析
最近的工作指出:Top Hessian eigenvalue(\(\lambda_{max}\))和Hessian trace(\(H_T\))适合作为性能预测和网络通用性指标,具有较低的\(\lambda_{max}\)和\(H_T\),说明该网络对于权重中的小扰动不太敏感,具有在训练期间,平滑损失空间、达到更平坦的最小值以及易于收敛的效果,这在FL中是非常有用的。
因此文章对于上述六种算法的\(\lambda_{max}\)和\(H_T\)进行了分析,有趣的是,文章发现了:正则化方法在降低这两个值是最有效的
最后,文章指出了:eigenvalue/trace的分析可以做为最优联邦学习的指导指标,他们提供了对landscape平整度和一致性的融合和聚集的促进。
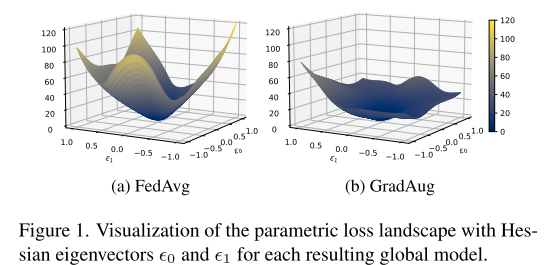
文章给出了一个结论:在模型试图减缓客户端飘逸和保持本地更新接近全局模型的过程中,似乎也阻止了他们充分学习少数异构甚至同构数据的能力。
方法
总体来说,文章发现了GradAug在FL设置中特别有效,在所有测试场景中精度最高,其中\(\lambda_{max}\)和\(H_T\)都是最低的,但是该方法大大增加了训练时间和本地计算量。因此本文设计了一个方法,提供了与GradAug相似的效果和性能,但大大减少了计算开销。
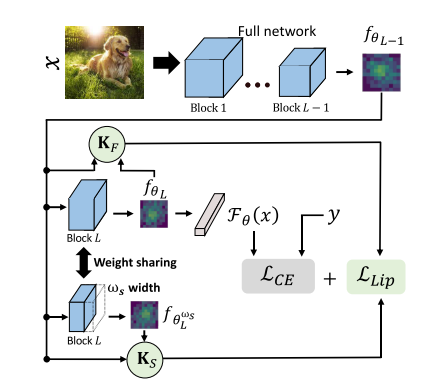
算法利用Hessian Eigenvalues作为模型在不同客户端上的相似性度量。
文章的目标函数为: \[ \mathcal{L}_{FA}=\mathcal{L}_{CE}(\mathcal{F}_\theta(x),y)+\mu\mathcal{L}_{Lip}(K_S,K_F) \] 其中\(\mathcal{L}_{Lip}\)是全宽子块\(L\)和减小宽度的子块的Liptschitz常数矢量(例如\(\lambda_{max}\))的均方误差。
Liptschitz常数矢量经由传输矩阵的谱范数来计算近似,传输矩阵如下:
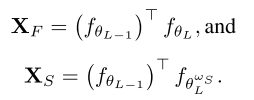
最后\(X_F\)和\(X_S\)的谱范数为\(K_F\)和\(K_S\)。

(🧐)Distilling the Knowledge in a Neural Network
Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. "Distilling the knowledge in a neural network." arXiv preprint arXiv:1503.02531 (2015).
在模型训练的时候,模型的重点在准确性上,所以对应于训练 ----> 笨重的大模型
在模型部署的时候,模型的重点在效率上,所以对应于部署 ----> 轻便的小模型
该文章提出了一个brand new的想法:大模型得出的logit,不仅仅是最后确定的类别是有意义的,其余类别的可能性也是有意义的。

举个很简单的例子:教师模型不仅仅可以给出这张图片有多么像马,稍微像一点驴,但是特别不像胡萝卜。
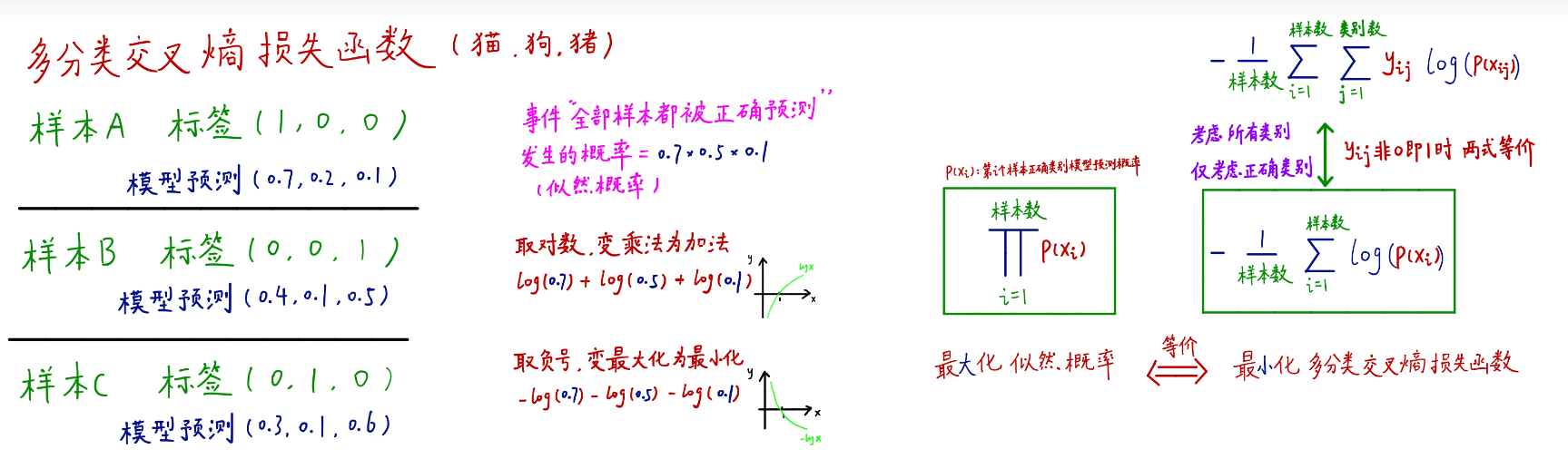
这是多分类交叉熵损失函数 ↑,训练的目的就是最小化该损失函数。
方法
一般来说,知识蒸馏可以用教师网络的soft target 作为学生网络的label。每个图片先输入到教师网络,然后利用教师网络的结果作为学生网络的输入。
此时会出现一些问题,即教师网络的输出不同类的可能性可能差距相当大,所以引入了蒸馏温度\(T\)来增大教师模型输出的熵。
基本构想:教师网络在\(T\)上获得的soft targets和学生网络在相同\(T\)下获得target进行拟合,越接近越好;或者将教师网络的输出当做学生网络的训练集。
知识蒸馏的好处:由于已经有教师网络,所以可以使用大规模的无标注数据集!
总loss是hard和soft的和,老师与书本都需要
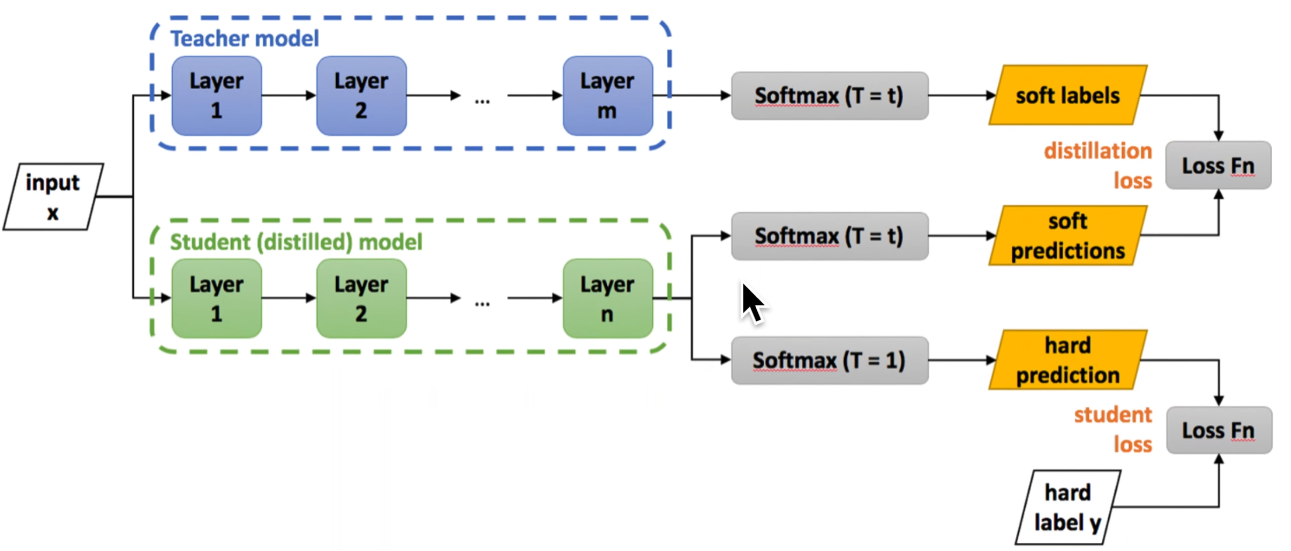


蒸馏温度\(T\)的作用: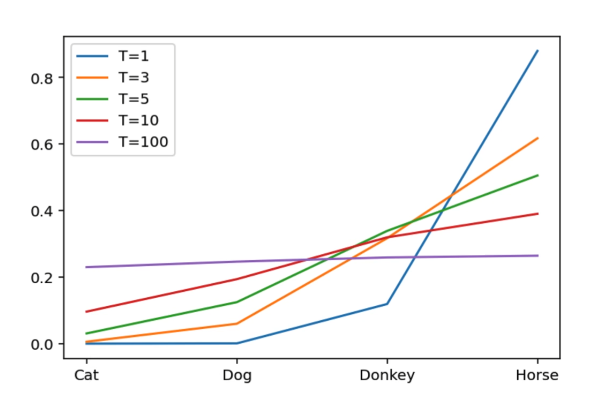
(🧐)SCAFFOLD: Stochastic Controlled Averaging for Federated Learning
Karimireddy, Sai Praneeth, et al. "Scaffold: Stochastic controlled averaging for federated learning." International conference on machine learning. PMLR, 2020.
文章提出了一种新的随机控制平均算法(SCAFFOLD)。创新点:
- 提出了一种新的随机控制平均算法(SCAFFOLD)来通过获得漂移量纠正客户端漂移。作者证明了SCAFFOLD至少和SGD一样快,并且可以收敛于任意异构的数据;
- 作者展示了SCAFFOLD还可以利用客户端之间的相似性来进一步减少所需的通信,这首次证明了采用本地步骤比大批量SGD的优势;
- 作者证明了SCAFFOLD相对不受客户端抽样的影响,从而使得它特别适合于联邦学习。
除此之外😁,文章还证明了:1. SCAFFOLD相对不受客户端抽样的影响,从而使得它特别适合于联邦学习;2. 作者给出了匹配的下界,以证明即使在没有客户端采样和全批处理梯度的情况下,由于客户端漂移,FEDAVG也可以比SGD慢。
👀解决的问题还是联邦学习中不同客户端的数据漂移。

证明部分
FedAvg的聚合
这个部分分为两个步骤:1. 本地更新模型;2. 聚合客户端的模型来更新服务器模型。
在每轮中,对客户端进行抽样,并对抽样中的每个客户端复制当前的服务器模型\(y_i=x\),并在\(K\)次本地更新中执行:\(y_i=y_i-\eta_lg_i(y_i)\),在运行结束后,进行全局聚合:\(x=x+\frac{\eta_g}{|S|}\sum_{i\in S}(y_i-x)\)。
这里面\(\eta_l\)是局部步长,\(\eta_g\)是全局步长。
文章将问题形式化为:最小化随机函数的总和 \[ min_{x\in R^d}\{f(x)=\frac{1}{N}\sum_{i=1}^{N}(f_i(x)=E_{\zeta_i}[f_i(x;\zeta_i)]\} \] 这里\(f_i()\)表示客户端的损失函数。文章假设\(f\)的下界是\(f^*\),\(f_i\)是\(\beta\)-光滑的,进一步文章假设\(g_i(x)=\nabla f_i(x;\zeta_i)\)是\(f_i\)的无偏差随机梯度,方差以\(\sigma^2\)为界。
对于满足上述条件的FedAvg,其输出在以下三种情况下均小于\(\epsilon\),\(R\)具有以下界限:

速率改善的原因主要是使用了两种不同的步长,通过更大的全局步长和较小的局部步长,可以减少客户端漂移。
异构性影响
本文也对客户端漂移对全局模型影响进行了说明。
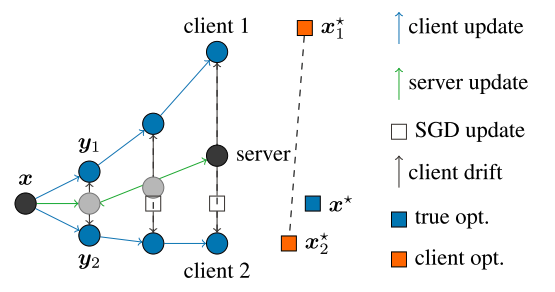
如图所示:
- 一开始服务器下发给客户端的模型是\(x\)
- 不同的客户端进行自己的训练,获得了\(y_1\)和\(y_2\),并利用FedAvg获得了灰色的全局模型
- 经过不断的训练,客户端1和客户端2的模型不断分散更新,FedAvg获得的模型为灰黑色圆圈
- 但是全局最优模型\(x^*\)是图中的方块,我们发现普通的平均聚合会导致全局模型与最优模型相差越来越多。
算法部分
在算法开始的时候,我们定义两个变量:\(c\):服务器控制变量;\(c_i\):客户端控制变量。
\(c\)是全局模型往最优模型的梯度下降方向,\(c_i\)是客户端的梯度更新方向
这两个变量的初始化可以均设置为\(0\),但是注意要保证\(c=\frac{1}{N}\sum c_i\),在每一轮的通信中,服务器参数\((x,c)\)被传输到了参与客户端\(S\subset [N]\)。
在最初始,每个客户端模型会复制服务器模型:\(y_i=x\),然后他在其本地数据上进行训练,执行K轮更新: \[
y_i=y_i-\eta_l(g_i(y_i)+c-c_i)
\] 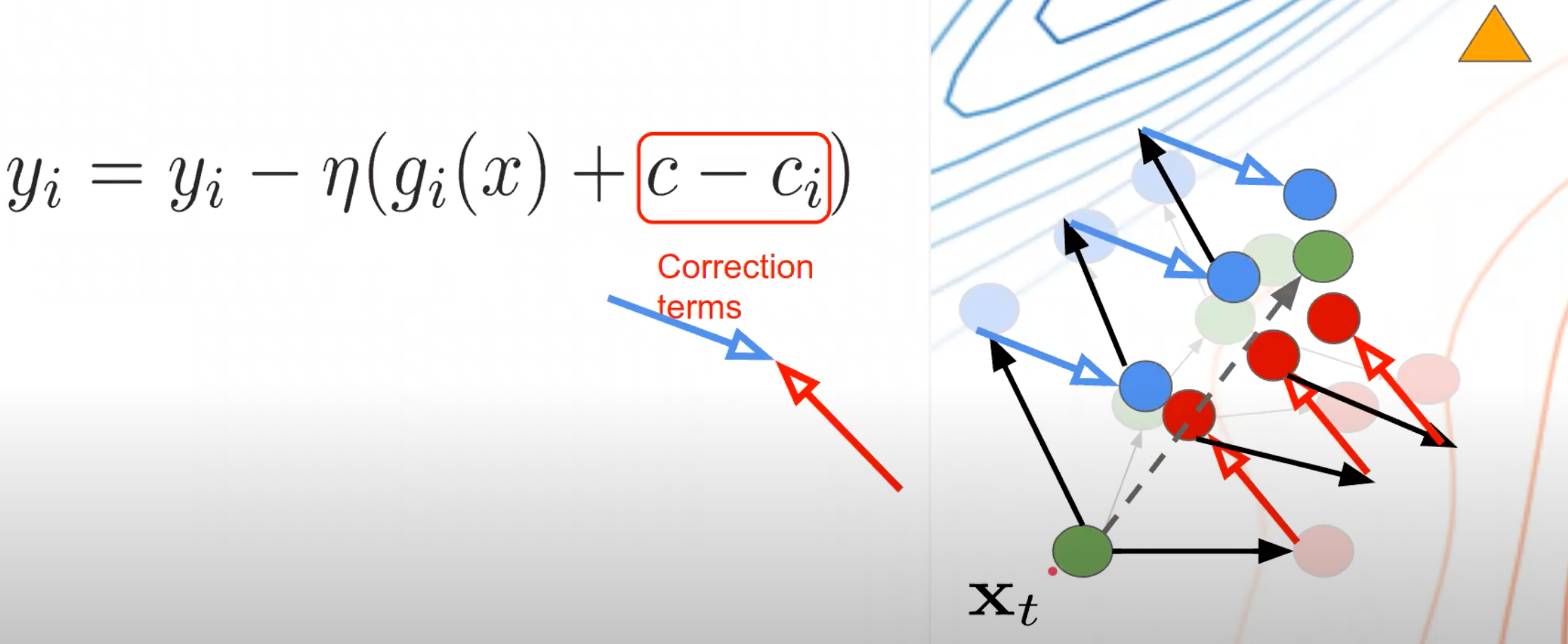
文章希望通过\(c\)和\(c_i\)让每个客户端的梯度更新方向向全局最优解的方向进行偏移。
然后,本地服务器控制变量将会得到更新 \[ c_i^+=\left\{ \begin{array}{**lr**} Option 1.\quad g_i(x), or & \\ Option 2.\quad c_i-c+\frac{1}{K\eta_l}(x-y_i). \end{array} \right. \]
第一种选择是计算服务器模型x处的梯度;第二个选择是重新使用先前计算的梯度来控制变量。第二种更👍🏻!
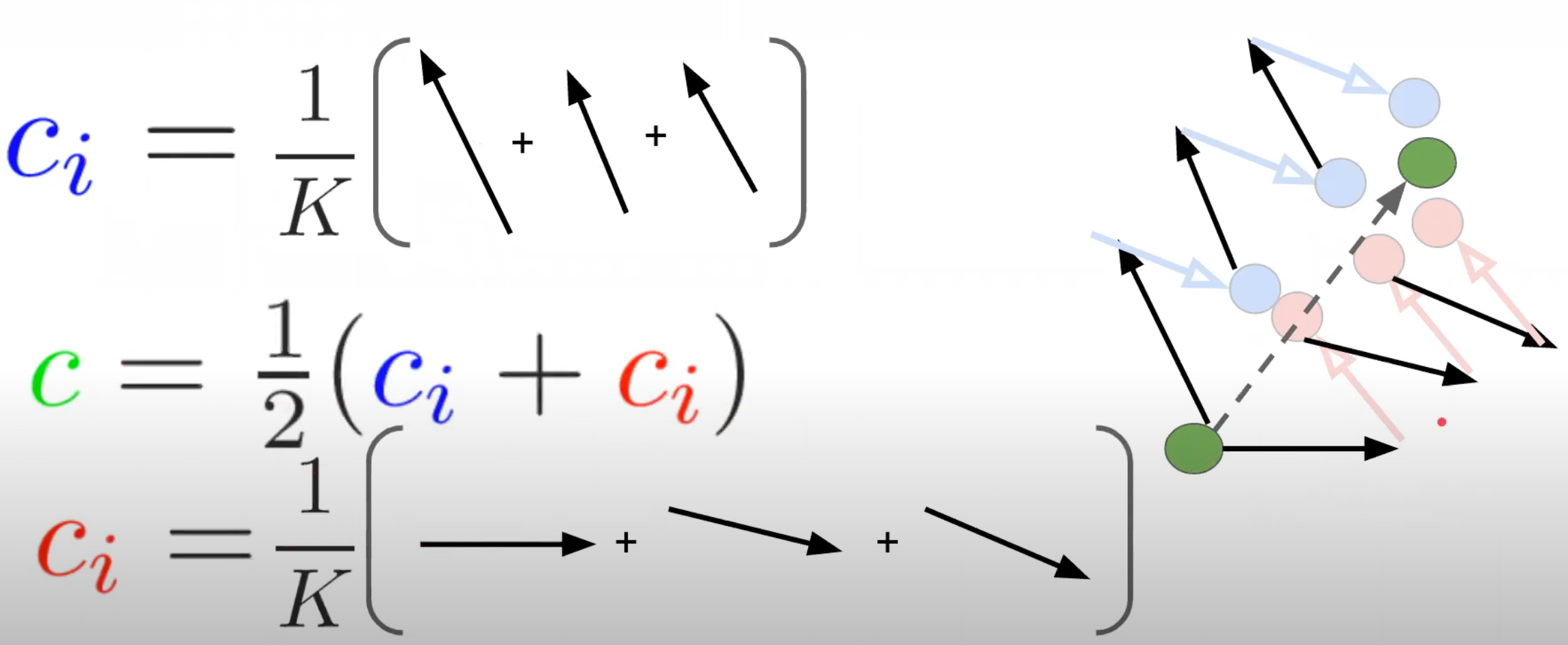
在这张图中我们看到,文章利用客户端在K次训练的梯度下降方向的平均值作为下次梯度下降方向的预测方向。
而全局模型向全局最优解的梯度下降方向近似于客户端梯度下降方向的平均值。
服务器层的更新方程: \[ x=x+\frac{\eta_g}{|S|}\sum_{i\in S}(y_i-x) \]
\[ c=c+\frac{1}{N}\sum_{i\in S}(c_i^+-c_i) \]
如果\(c_i\)总是被设置为0,那么则是传统的FedAvg。
如果不考虑通信成本,那么客户机上的理想更新应该为 \[
y_i=y_i+\frac{1}{N}\sum_jg_j(y_i)
\] 文章模型利用控制变量获得了 \[
c_j\approx g_j(y_i)\quad and\quad c\approx \frac{1}{N}\sum_j g_j(y_i)
\] 因此: \[
(g_i(y_i)-c_i+c)\approx \frac{1}{N}\sum_j g_j(y_i)
\] 

Addressing Heterogeneity in Federated Learning via Distributional Transformation
Yuan, Haolin, et al. "Addressing heterogeneity in federated learning via distributional transformation." European Conference on Computer Vision. Cham: Springer Nature Switzerland, 2022.
文章提出了联邦学习分布式转换框架,称为DisTrans。创新点:
- 其不仅仅通过漂移量更改模型,与此同时还通过漂移量更改数据;
- 设计了双通道的神经网络结构;
- 提出了\(DH\)异构量化,并利用神经网络进行聚合。
👀解决的问题是联邦学习中的客户端漂移
动机
利用漂移量转换每个客户端的训练和测试数据,来提高异构数据下的联邦学习,为了证明其可行性,文章利用了两个例子。
对于非凸训练模型
假设\(f(x)=cos(wx)\),对于每个客户端,通过本地数据\(x\)获得\(y\):\(y=cos(w_{client_k}^{true}x)+\epsilon_{clinet_k}\),其中\(x\)是从高斯分布中绘制的IID数据,\(\epsilon_{clinet_k}\)是均值为0的高斯噪声,漂移量为\(px+q\),\(p\)是连个客户端处的固定值,\(q\)是通过暴力搜索来选择的。图(a)显示了有漂移的模型更加一致。
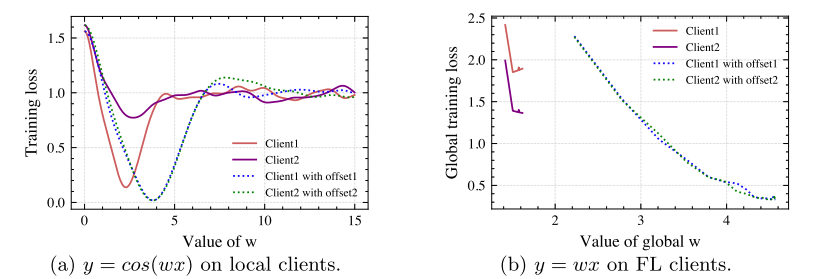
聚合服务器的线性回归问题
作者训练了两个局部线性模型,\(f(x)=wx\),在服务器上进行聚合,重复联邦学习步骤直到收敛。本地训练数据是异构的,生成\(y=w^{true}_{clinet_k}x+\epsilon_{clinet_k}\)。当存在漂移时,聚合模型收敛。
方法

在每一轮中,每个客户端学习一个本地模型和一个漂移量,并将其发送给服务器。服务器聚合客户端的本地模型和漂移量,并将其送回客户端。
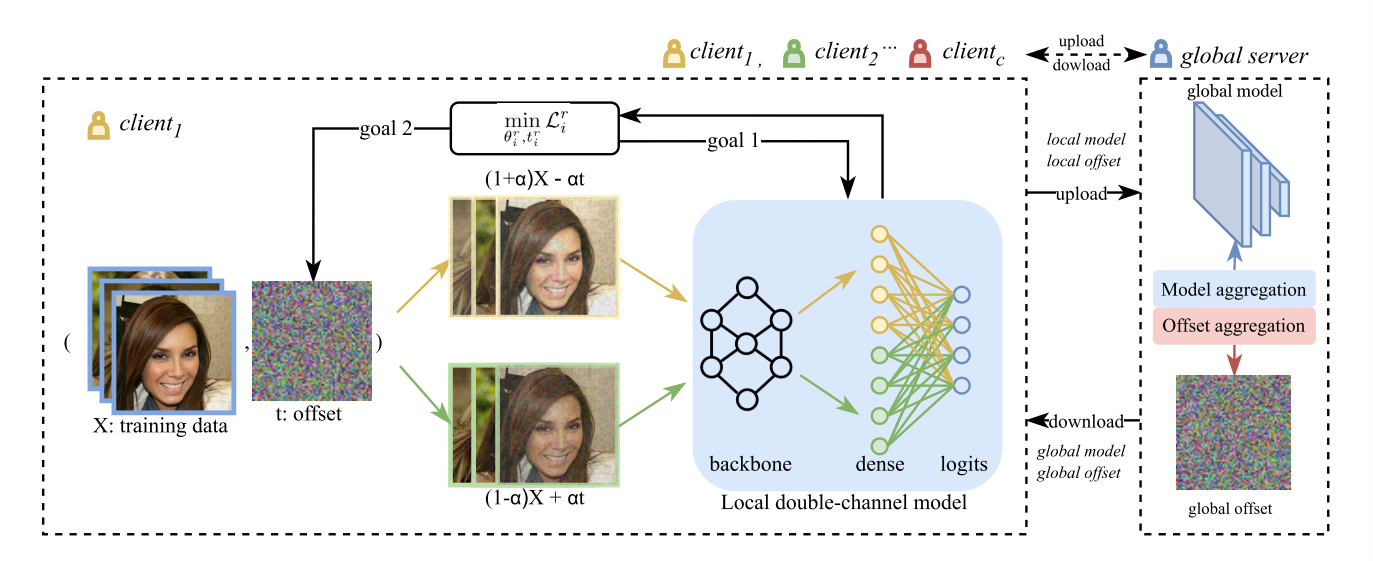
对于本地、全局模型,DisTrans使用了双输入通道神经体系结构,如上图所示
文章的神经网络架构有一个共享的backbone,一个密集层链接两个通道的输出,一个logit层合并输出。这两个通道使用相同的漂移量\(t\),以两种方式移动本地数据分布: \[ x_t=((1-\alpha)x+\alpha t,\quad(1+\alpha)x-\alpha t) \] 在优化中,每个客户端的目标是实现以下两个目标:
- 优化漂移量,使局部数据更符合局部模型
- 优化局部模型以适应便宜的局部数据分布
这和别的文章不一样,本文章是数据和模型同时漂移。
将这两个目标合一获得以下目标方程: \[ min_{\theta_i^r,t_i^r}L_i^r=\frac{1}{N}\sum_{z_t\in D_{ti}}l(\theta_i^r,z_t) \] 其中\(\theta_i^r\)为客户端\(i\)的模型,\(t_i^r\)是客户端\(i\)的漂移量,\(L\)是客户端的损失函数(交叉熵损失),\(z_t=(x_t,y)\)是训练样本用漂移量进行漂移,\(D_{ti}\)是对于客户端\(i\)漂移后的局部训练数据集。
获得\(\theta\)是为了解决Goal 2,获得\(t\)是为了解决Goal 1。
聚合
文章采用了基于度量的偏移量聚合方式,其提出了一种对异构性的度量方式: \[ DH=1-\frac{\sum_{j\in [1,N]}c_j}{N\times C} \] \(N\)是所有的类别,\(C\)是客户端数量,\(c_j\)的定义如下: \[ c_j=\left\{ \begin{array}{**lr**} 0,\quad if\space only\space one \space client\space has\space data\space from\space class\space j\\ k,\quad if\space k>1\space clients\space have\space data\space from\space class\space j \end{array} \right. \] \(DH\)是一个\([0\%,100\%]\)的量,DisTrans在聚合的时候,如果分布异构性非常大,一个客户端的漂移量可能无法为另一个客户机的漂移量提供信息,因为他们俩数据分布有本质区别,因此文章只会在异构性小于\(50\%\)时聚合客户的偏移量。
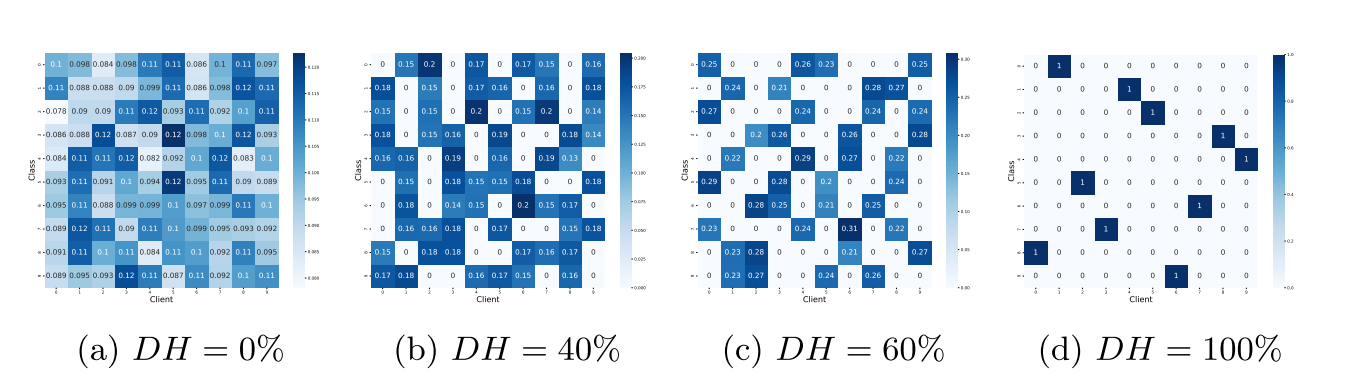
假设联邦学习系统的异构性小于阈值。聚合客户端漂移量的一种简单方法是将其平均值作为全局偏移量计算,然后将其发送回所有客户端。然而,这种朴素的聚合方法对所有的客户端使用相同的全局漂移量,从而达到了次优精度。
因此,文章提出了基于神经网络的聚合方法。
其将客户端特定的嵌入向量\(e\in R^{1\times N}\)和客户端偏移量作为输入,并为客户端输出一个聚合的偏移量:其中嵌入向量的条目\(e_i\)就是客户端对类别\(i\)的训练数据的训练分数。服务器在训练过程中将聚合作为一个回归问题来学习。在每一轮中,服务器收取一组\((t_i,t'_i)\),其中\(t_i\)是当前轮钟来自客户端\(i\)的漂移量,\(t'_i\)是上一轮的漂移量,服务器利用SGD来最小化两者的距离。
(Similar)Accelerating Federated Learning With Cluster Construction and Hierarchical Aggregation
Wang, Zhiyuan, et al. "Accelerating federated learning with cluster construction and hierarchical aggregation." IEEE Transactions on Mobile Computing (2022).
文章提出了FedCH,其构建了一种特殊的集群拓扑结构进行分层聚合训练。创新点为:
- 提出了一种新的FL机制来解决边缘计算中的资源约束和客户端异构
- 提出了一种算法来确定资源约束下的最佳集群数量,并构建分层拓扑结构
👀文章解决的问题是:联邦学习可能导致的网络拥塞、客户端资源有限且异构、客户端上计算资源有限
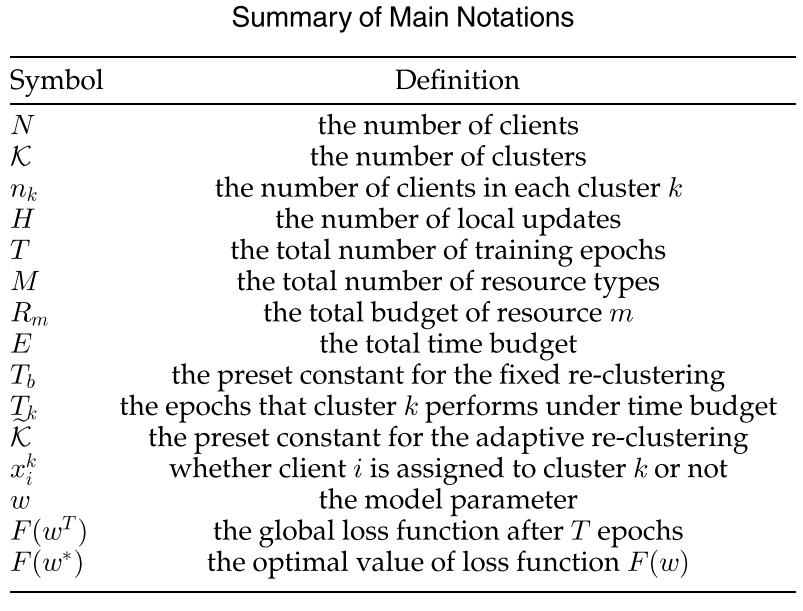
算法部分
和BGFL很相似,FedCH的训练过程分为三个步骤:本地模型更新,集群内聚合,全局聚合。
和BGFL不同的地方是:由于FedCH是异步联邦学习,其在分组的时候认为,群组内的设备是同步联邦学习;群组间是异步联邦学习。
因此其全局聚合的部分采用了异步操作。具体流程如图所示:
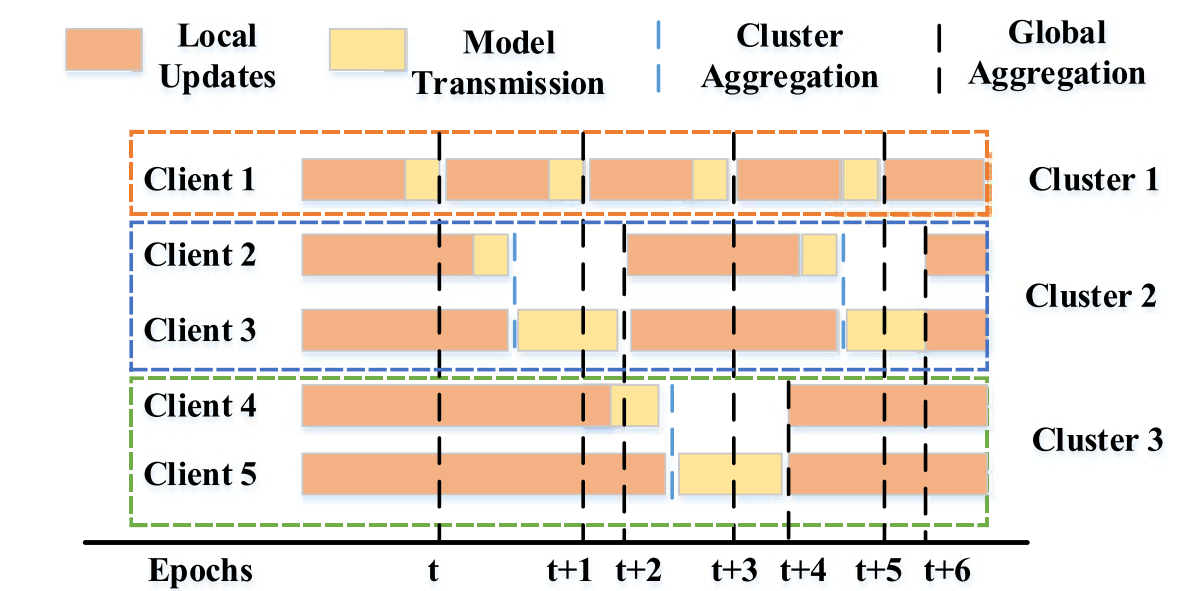
现在有五个客户端,每个条的长度表示相应操作的时间消耗。
- 首先基于他们的异构训练速度将五个客户端分配到三个集群中,即:a. 组一:1;b. 组二:2,3;c. 组三:4,5
- 每个组独立执行训练过程,不同的组有不同的全局聚合频率。(三个集群分别经历了:4,2,1次全局聚合)
对于Cluster 2,假设客户端3被选择为集群leader,在训练期间,客户端2将更新的本地模型发送到3用于群组聚合,客户端3将聚合后的模型发送给服务器进行全局聚合。

异步全局聚合
在异步联邦学习中,由于不同群组的训练完成时间不同,所以就会出现比较新的更新和比较老的更新。文章对此加入了陈旧性处理。对于每一次更新,参数更新函数为 \[ \omega^t=(1-\alpha_\tau^t)\omega^{t-1}+\alpha_\tau^t\omega(k) \]
\[ \alpha_\tau^t=\left\{ \begin{array}{**lr**} \alpha,\quad \tau \leq a\\ \alpha\cdot\tau^{-b},\quad \tau > a \end{array} \right. \]
该函数意味着当超过\(a\)时,模型的权重会随着老化程度的增加迅速下降;同时,每个群组的模型权重应该随着群组数量的增加而下降,所以我们对\(\alpha\)的初始化为\(\frac{K-1}{N}\)。
分组方法
如果是用简单的K-means方式进行分组,会有以下几种问题:
- k-means独立、平等地对待对象的所有属性,然而,对于两个属性(比如计算和通信)对不同模型的效率有不同的影响。
- 除了初始化过程中的K个聚类的质心,每个聚类的质心可能是迭代期间给定具有属性值的虚拟对象,而不是真正的客户端。
- K-means算法使得每个集群的客户端数量在\([1, N-K+1]\),在某些情况下,集群可能会出现只包含一个客户端的情况
本文的分组方式:
分组目标:
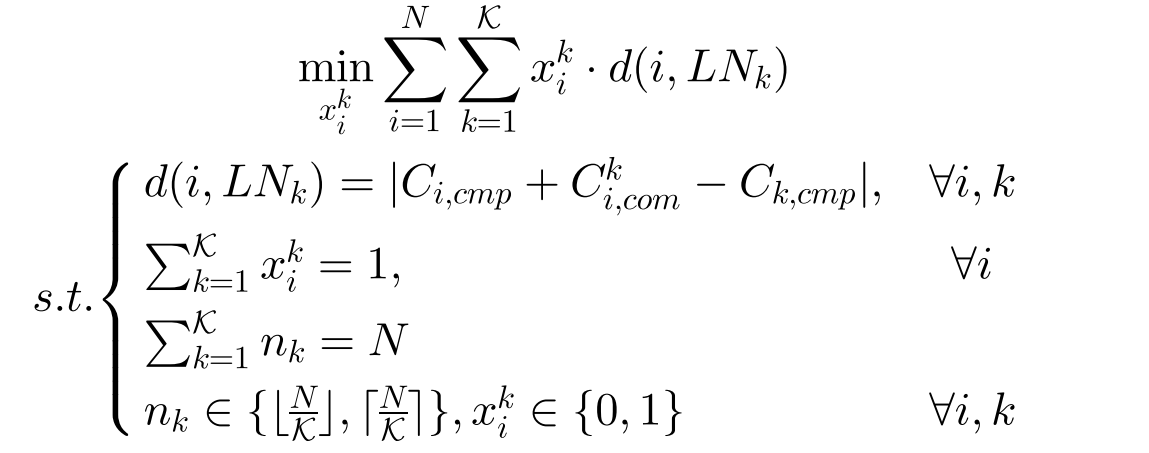
- \(C_{i,cmp}=H\frac{|D_i|f}{f_i}\),训练时间
- \(C_{i,com}=\frac{M}{B_{i,k}}\),通信时间
- \(LN_k\)为这个集群的leader,F对客户端\(i\)与leader的不相似度量设定为:\(d(i,LN_k)\)
在聚类算法中,我么你讲每个客户端与相应的leader相匹配。由于在这个匹配问题中只有两种类型的实体,因此采用了二分图来解决。
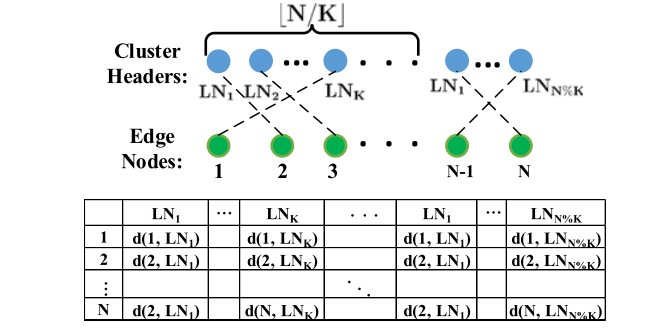
文章将集群分成了两个大组,第一组是\(1\leq k \leq N\%K\),第二组是\(N\%K \leq k \leq K\)。
第一大组中每一个群组有\(\lfloor N/K\rfloor + 1\)个节点,第二大组每一个群组有\(\lfloor N/K\rfloor\),总共有\(N\)个节点。
同样的,文章也将客户端分成了\(N\)个节点,所以为了找到最优的聚类结构,等价于找到这两个图的最大匹配。文章构建了一个\(N\times N\)的矩阵\(A\),其中每个元素表示对应客户端和集群leader之间的距离。文章搜索\(A\)中不同行和列的\(N\)个值,使其和最小。在文章中用的是匈牙利算法进行二分图匹配。具体算法如下所示:

- 初始化(1-2):我们从\(N\)个节点中选择\(K\)个任意客户端作为每个集群的质心,并创建矩阵\(A\)。
- 聚类构造(4-10):计算\(d(i,LN_K)\),并将其赋值到\(A\),之后通过匈牙利算法聚类
- 集群拓扑调整(11-16):在将每个客户端分配到集群中后,更新每个集群的质心,选择集群内所有节点到其距离最近的点作为质心。
上面的算法将会不断迭代,直到集群结果不再改变或者目标函数不在减少。
重新聚类
文章提出了动态聚类的方式,其设置了一个\(t_b\)作为重新聚类触发器的阈值,如果\(T_b > t_b\),则开始重新聚合,如今\(t_b\)的最佳数值还需要进行讨论。
如果\(K\)很小,则说说明每个群组中的客户端数量很多,导致离散情况越容易发现,所以阈值应该设置较小
如果\(K=1\)或者\(K=N\),则阈值设置为无穷大,因为不会再进行分组。
如果是单独使用阈值聚类,无法适应网络状态的突然恶化。对此,文章提出了一种自适应重新聚类。
服务器将采用\(s_k\)来记录每一个集群\(k\)的掉队情况,如果出现了掉队者则设置\(s_k=1\)(比如,集群\(k\)两次全局聚合的时间大大增加),反之为\(0\)。当\(\sum s_k\)到达一定数量的时候,重新聚类算法将会被激活。激活后所有的\(s_k\)会被重置回\(0\)。
证明部分
该文章证明了\(K\)的最佳取值,如果需要分组,可以详细看一看。
(Similar)FedHiSyn: A Hierarchical Synchronous Federated Learning Framework for Resource and Data Heterogeneity
Li, Guanghao, et al. "FedHiSyn: A hierarchical synchronous federated learning framework for resource and data heterogeneity." Proceedings of the 51st International Conference on Parallel Processing. 2022.
也是分层聚合联邦学习,创新点是:聚类中采用了环形的拓扑结构进行聚合。
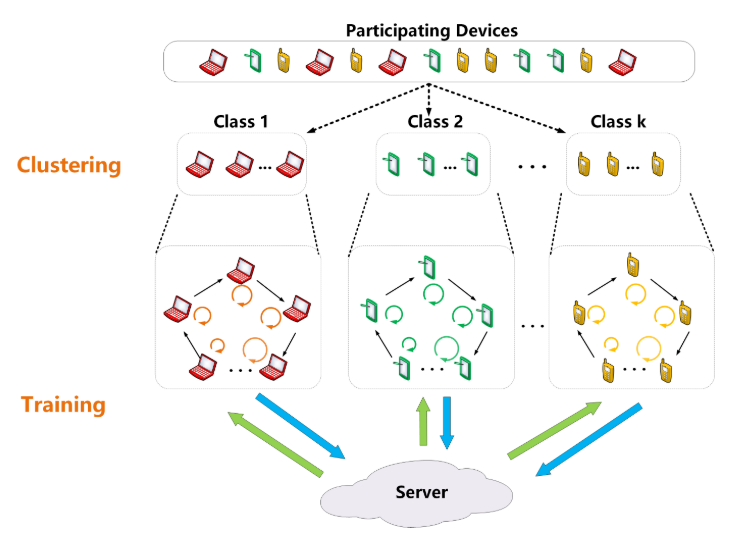
文章将计算能力相近的设备分成同一个群组\(\{class_1,class_2,...,class_k\}\),其中\(class_1\)是计算最快的组别,\(class_k\)是计算最慢的组别。
在每一个组中,也按照计算能力强弱进行由快到慢的排序,最慢的设备连接到最快的设备完成环形拓扑结构。当本地设备完成训练后,会将模型按照环形拓扑的方向传递给下一个模型。
具体来说,在每个训练轮开始的时候,服务器向每个设备发送初始化参数,每经过\(R\)次,服务器会聚合其接收到的更新模型来完成一轮的训练。
- 设备从服务器接受模型,进行本地训练以更新模型
- 设备根据环形拓扑将更新后的模型发送个下一个设备
- 设备接收到上一个设备发送的模型后,在本地训练接收到的模型来完成模型更新。如果没有接收到,则继续训练本地上次训练的模型。
- 重复2-3,直到时间\(T\),所有设备将本地模型上传到服务器完成一轮训练。

由于每一个模型都是在各个设备中循环训练,所以聚合的时候不能采用数据量的方式进行聚合。因为训练时间更快的群组\(class_1\)可以经过更多轮的通信,为了避免不让聚合参数偏向这些本地训练时间较短的设备,文章采用了将设备完成本地训练的平均时间作为聚合权重。 \[ W_G^{r+1}=\sum^{||S||}_{i=1}\frac{l_i}{L}W_i^{r+1} \]
(Similar)Blockchain-Based Two-Stage Federated Learning With Non-IID Data in IoMT System
Lian, Zhuotao, et al. "Blockchain-based two-stage federated learning with non-IID data in IoMT system." IEEE Transactions on Computational Social Systems (2022).
提出了基于区块链的两阶段联邦学习方法,创新点:
- 基于区块链的数据共享策略
- 客户端选择方案来减少通信开销
解决的问题:在共享子数据集的时候,可能会有一些客户端共享虚假的子集;客户端不希望共享的数据被第三方服务提供商访问;还会出现梯度翻转攻击等恶意行为,所以要保护客户端和服务器的隐私。
算法层面
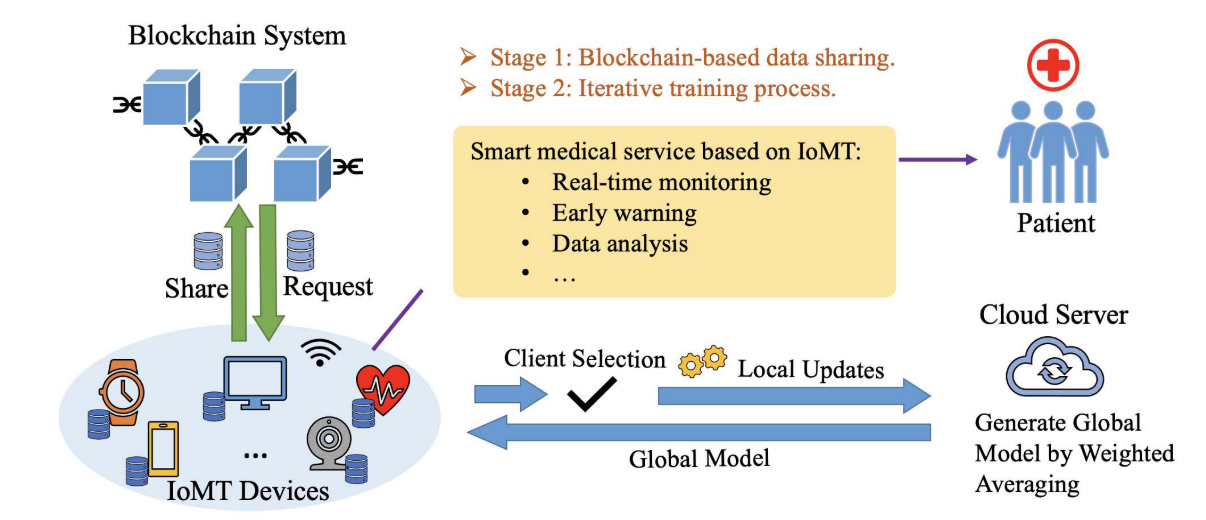
- 文章首先构造一致的小型全局共享数据集来减少非IID
- 文章在收集全局数据集的同时,通过区块链加强隐私保护
- 文章还利用了客户端选择算法在联邦学习中选择高质量的客户端
文章的工作流程如下:
- 一阶段:通过区块链系统构建全局共享数据集。
- 标识参与联邦学习的客户机,并初始化区块链。
- 客户端将小规模\(\alpha\)的本地数据\(D_\alpha\)上传到区块链系统。
- 区块链系统合成全局共享数据集。
- 客户端将共享数据集集成到本地数据中。
- 二阶段:通过客户选择提高非IID数据训练性能。
- 服务器选择部分客户端参与全局训练。
- 每个选定的客户端都使用全局共享数据集和本地数据集来训练本地联邦学习模型。
- 本地培训完成后,客户端将培训结果上传到服务器。
- 服务器根据来自参与客户机的本地更新执行全局聚合,以生成新的全局模型。
- 服务器将新模型分发到客户机设备,以更新它们的本地模型。
小规模数据共享
为了避免有些客户端会上传恶意的数据集子集,服务器应该能在不访问数据集的情况下指导这个数据集的来源。必须要保证参与数据共享的用户是可以控制和可追踪的。
因此文章采用区块链系统实施数据集共享,首先只有选定的客户端才能参与数据共享,参加到区块链网络,由于数量少,所以共识速度也会很快。通过区块链共享数据可以限制其他用户对原始数据的访问,从而保证隐私。
系统在选择参与全局数据共享的客户端之后,为其建立一条公共区块链。当用户作为数据共享者参与时,可以通过PoW机制计算哈希值,向区块来拿发送共享事务请求。然后客户端将在区块链系统中生成一个区块,并上传本地数据的\(\alpha\)部分;当用户作为数据请求者参与,客户端向区块链发送下载数据请求,验证通过后客户端才可以下载。区块链数据共享如图所示:
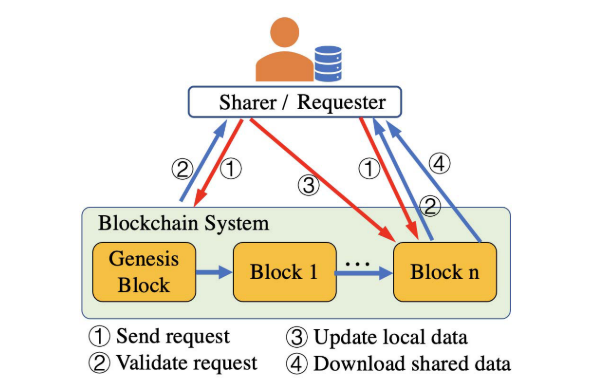
在客户端下载共享信息之后,将共享数据和本地数据组合:\(D_i=D_i+D_g\),那么全局优化目标则是: \[ argmin_{\omega_t}\sum_{i=1}^mp_jl(D_i+D_g,\omega^i) \]
客户端选择
在使用非iid数据的联邦学习中,共享数据集的质量直观地反映了训练性能。如果共享数据集不是均匀分布的,而是有偏置的,可能会降低局部训练模型的鲁棒性,影响全局模型训练结果。数据共享阶段已经消耗了客户机的计算能力来保证隐私。因此,必须保证共享数据集的均匀分布和高质量。
为了获取最有效的数据,文章需要获取本地数据集的相关性。
- 文章在客户端生成最具有分布式特征的子数据集
- 记录每个客户端子数据集的相似度得分,利用JS散度,越接近1,越说明相似度越低
- 首先选择相似度得分较低的客户端来进行训练
寻找最具分布式特征的子数据集:选择相似度较低的数据放入共享数据集子集中
